Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fluxo de Campo Elétrico

Ver Teoria
Exercício 1234567891011121314151617181920212223242526272829303132333435363738394041424344454647

Enunciado

Um campo elétrico dado por:

E → = 4 . i ^ - 3 . y 2 + 2 j ^

Atravessa um cubo com 2 m de aresta posicionado na forma demonstrada na figura. ( E é dado em newtons por Coulomb e x em metros). Determine o fluxo elétrico:

(a) através da face superior,

(b) através da face inferior,

(c) através da face da esquerda,

(d) através da face da traseira.

(e) Qual é o fluxo elétrico total através do cubo?

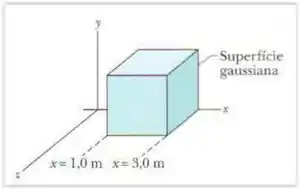
Passo 1

O fluxo do campo elétrico em uma superfície é dado por

Φ = ∫ E → ⋅ d A →

Quando o campo é constante ao longo da superfície

Φ = E → ⋅ A →

Onde A → é o vetor normal à superfície e que tem módulo igual a área da superfície. Como é um cubo de lado 2 m , a área de cada face é 4 m 2 . Assim, o módulo do vetor área vale 4. A direção e o sentido dele vão ser dadas de acordo com cada face. Acompanha aqui comigo.

Passo 2

Começando pela parte mais fácil, as faces de frente e de trás:

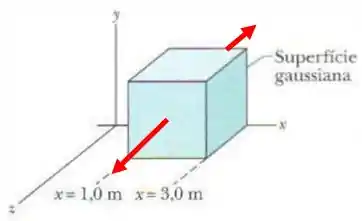
A normal dessas faces estão na direção ± k ^ . Assim o nosso fluxo pra esses dois caso vai ser\

Φ = E → ⋅ A →

Φ = 4 . i ^ - 3 . y 2 + 2 j ^ ⋅ ± 4 k ^

Como o produto interno entre o campo e o vetor normal de ambas as faces vão ser zero, temos:

Φ F R E N T E = Φ A T R A S = 0

Passo 3

Agora vamos olhar pras faces da esquerda e da direita:

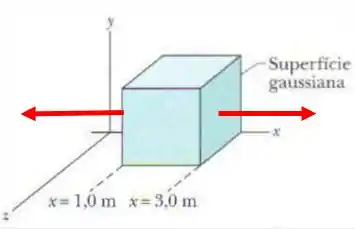
Pra face da esquerda a normal tá na direção - i ^ , enquanto que pra face da direita a normal tá na direção i ^ . Assim

Φ E S Q U E R D A = 4 . i ^ - 3 . y 2 + 2 j ^ ⋅ - 4 i ^ = - 16   m 2 N / C

E

Φ D I R E I T A = 4 . i ^ - 3 . y 2 + 2 j ^ ⋅ 4 i ^ = 16   m 2 N / C

Passo 4

Agora na face de cima e na de baixo os vetores normais estarão nas direções ± j ^

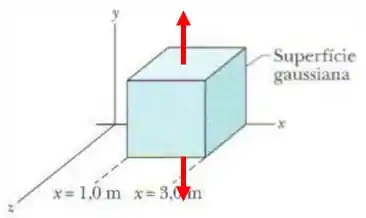
Na superfície de cima

Φ C I M A = 4 . i ^ - 3 . y 2 + 2 j ^ ⋅ 4 j ^ = - 12 ( y 2 + 2 )

E caraca.... sobrou um y no final da conta! Pra sumir com ele basta substituir o seu valor! Na superfície de cima y tem um valor constante que é 2 . Assim

Φ C I M A = - 12 y 2 + 2 = - 12 2 2 + 2

Φ C I M A = - 72   m 2 N / C

Já na superfície de baixo

Φ B A I X O = 4 . i ^ - 3 . y 2 + 2 j ^ ⋅ - 4 j ^ = 12 ( y 2 + 2 )

O valor de y nessa superfície é 0

Φ B A I X O = 12 y 2 + 2 = 12 0 2 + 2

Φ B A I X O = 24   m 2 N / C

Passo 5

Vamos interpretar o resultado. É verdade que a questão não pediu todos os fluxos, mas o legal de fazer isso é que vamos poder interpretar o problema. Representando os fluxos em uma tabela:

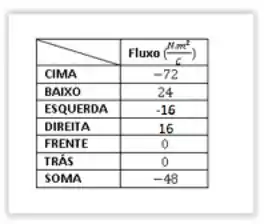
Podemos ver que a soma não dá zero. Isso significa, fisicamente, que existe alguma carga dentro do cubo ;)

Resposta

(a) através da face superior, - 72 N . m 2 C

(b) através da face inferior, 24 N . m 2 C

(c) através da face da esquerda, - 16   N . m 2 C

(d) através da face da traseira, 0

(e) Fluxo elétrico total através do cubo:   - 48   N . m 2 C

Exercícios de Livros Relacionados

15.8E As duas pequenas esferas metálicas vistas na Figura 15.16, de mesmo raio, estão suspensas por fios finos de náilon.Mostre que θ ' = θ . (B) Imagine que um fino fio condutor faça contato simultân
O fluxo de campo elétrico em cada face de um dado tem um valor absoluto, em unidades de 10 3 N · m 2 / C , igual ao número N de pontos da face ( 1 ⩽ N ⩽ 6 ). O fluxo é para dentro se N for ímpar e par
Um cubo possui arestas com comprimento L e é colocado com um dos vértices na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, porém é dado por E → = - B i ^ + C j ^ - D k ^ , onde
O campo elétrico E → 1 em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico E → 2 também é uni
Uma superfície plana quadrada com lado igual a L é descrita pelas equações a Faça um desenho do quadrado e mostre os eixo x ,y e z . b Calcule o fluxo elétrico através do quadrado produzido por uma ca