. Uma esfera isolante de raio está carregada de forma que seu hemisfério superior possui uma densidade volumétrica de carga constante e positiva enquanto seu hemisfério inferior possui uma densidade volumétrica de carga constante e negativa . Considere uma superfície imaginária e fechada na forma de um hemisfério de raio , como mostra a figura abaixo. Esta superfície é composta por uma superfície hemisférica aberta , que define o hemisfério, e pela base plana , que divide as regiões de carga positiva e negativa da esfera.
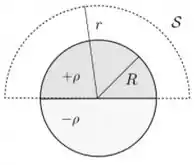
Sobre essa situação, considere as afirmativas abaixo:
O campo elétrico produzido pela esfera tem módulo constante em todos os pontos da superfície hemisférica aberta .
O campo elétrico produzido pela esfera é perpendicular a todos os pontos da base plana .
O fluxo do campo elétrico produzido pela esfera através de vale .
É (são) VERDADEIRA(S) a(s) afirmativa(s):
Escolha uma opção:
Nenhuma delas
e
e
e
e
Passo 1
Vem comigo que a gente resolve essa juntos!
Para podermos avaliar as afirmações temos que entender como o campo elétrico da esfera se comporta.
Dentro dela o campo é nulo e a gente pode ver isso usando a lei de Gauss para usa superfície esférica de raio , teríamos:
E a carga interna a essa superfície é zero já que temos densidades de carga iguais e de cargas opostas.
Fora da esfera teremos linhas de campo que saem da parte positiva e vão para parte negativa, então campo fora da esfera, mas se usarmos uma superfície fechada esférica (por conveniência) e calcularmos o fluxo usando a lei de Gauss vemos que ele é nulo.
Então cada hemisfério da esfera produz um campo igual e uniforme, como se fosse uma esfera com densidade de carga ou .
Com isso podemos avaliar as afirmações.
Passo 2
Vamos avaliar a primeira afirmação.
Como já vimos o campo elétrico fora da esfera é se comporta como se fosse de uma esfera com densidade de cara e um campo desse tipo tem o mesmo módulo para distâncias iguais a superfície, então de certa maneira o módulo dele é constante em toda superfície .
Então a afirmativa é verdadeira.
Passo 3
Vamos analisar a segunda afirmação.
No passo um vimos que o campo dentro da esfera é zero, então não faz sentido ele ter uma direção dentro dela.
Logo essa afirmação é falsa.
Passo 4
Para calcular o fluxo através de teríamos que somar o fluxo através de e .
Já podemos dizer que através de é zero já que não temos campo dentro da esfera, então o fluxo através de é igual ao de .
O fluxo de vai ser igual a metade do fluxo através de uma superfície esférica de raio e densidade , pela lei de Gauss, temos:
A carga interna é igual a densidade de carga vezes o volume da esfera, assim:
Então:
Como estamos interessados em metade disso, temos:
Então a afirmação é verdadeira.
Então as únicas afirmações verdadeiras são a e , então nossa alternativa vai ser a letra .
Resposta
e