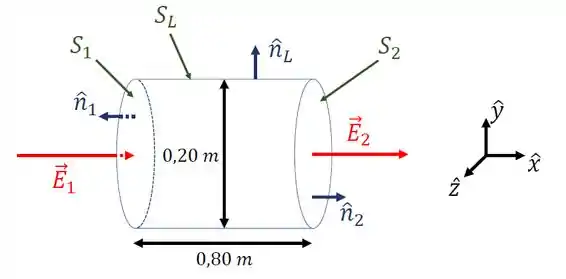
Um campo elétrico não-uniforme é direcionado ao longo do eixo em todos os pontos no espaço. A magnitude do campo varia com , mas não com respeito a ou . O eixo de uma superfície cilíndrica, com de comprimento e de diâmetro, é alinhado paralelamente ao eixo , como mostrado na figura abaixo. Os campos elétricos e , nas extremidades da superfície cilíndrica, têm magnitudes de e , respectivamente, e são dirigidos como mostrado. Quanto vale, aproximadamente, o fluxo elétrico que passa pela superfície cilíndrica?
(a)
(b)
(c)
(d)
(e)
Passo 1
Primeiramente, vamos lembrar a definição do fluxo de um campo elétrico.
O fluxo de um campo elétrico por uma superfície genérica é dada por
sendo um vetor unitário normal ao elemento infinitesimal de área .
ATENÇÃO!! Esta não é a lei de Gauss!! A lei de Gauss se refere ao fluxo do campo elétrico por uma superfície FECHADA!!
Aplicaremos essa definição nas tampas e na lateral da superfície cilíndrica para determinar o fluxo total. SIMBORA!
Passo 2
O fluxo total do campo elétrico pela superfície cilíndrica é dado por
com e os fluxos do campo elétrico pelas superfícies e , respectivamente, dados por
e o fluxo do campo elétrico pela lateral da superfície cilíndrica , dado por
Os vetores , e são vetores unitários normais às superfícies , e , respectivamente, como mostrado na figura do enunciado.
Para continuar, devemos fazer uma análise: o enunciado diz que o campo elétrico é não-uniforme, mas não depende de nem de , apenas de . Isso significa que em todas as superfícies paralelas ao plano (tampas da superfície cilíndrica), o campo elétrico possui o mesmo valor, isto é, o mesmo módulo.Isto não significa que o campo é constante!!! O campo elétrico pode ter direções e sentidos diferentes.
Resumindo: não sabemos a direção e o sentido do campo elétrico sobre as tampas (sabemos apenas os módulos, dados no enunciado). Além disso, não sabemos NADA sobre o campo elétrico dentro da superfície cilíndrica (nem direção, nem sentido e nem módulo)!!
UÉ PAULO!! MAS ENTÃO COMO A GENTE FAZ ?!??!
Calma! A gente vai ver como faz no próximo passo. 😊
Passo 3
Para contornarmos todos os problemas que apareceram, faremos uma aproximação (por isso que o enunciado diz “aproximadamente”, sacou?).
Vamos supor que o campo elétrico na região do cilindro seja apenas na direção , isto é,
Note que essa aproximação não é tão absurda. Como os campos nas superfícies de e são paralelos ao eixo , então é de se esperar que o comportamento médio do campo elétrico seja apenas na direção .
Mas Paulo, no que essa aproximação ajuda? Bom.. ela RESOLVE A PARADA!! Vamos ver como.
Vejamos novamente a figura do enunciado.
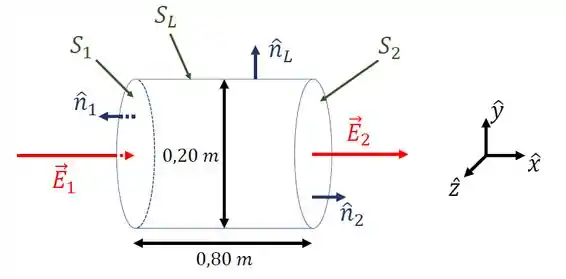
Na superfície , temos que o ângulo entre e é . Assim,
com o módulo do campo elétrico na superfície .
Na superfície , temos que o ângulo entre e é . Assim,
com o módulo do campo elétrico na superfície .
Na superfície , temos que o ângulo entre e é . Assim,
Desta forma, temos que os fluxo , e são dados por
sendo e as áreas das superfícies e , respectivamente. Viu como a aproximação resolveu?? AHAHAHA
Para a gente continuar, precisamos das áreas e . Vamos obtê-las no próximo passo.
Passo 4
Vamos agora determinar as áreas das tampas da casca cilíndrica.
Vemos que as superfícies são círculos. Assim,
sendo o diâmetro dos círculos.
O enunciado diz que . Logo,
No próximo passo determinaremos os fluxos e , além do fluxo total . Bora gente!!
Passo 5
Vamos determinar cada fluxo agora.
O enunciado diz também que e . Logo, os fluxos e são dados por
Com isso, podemos determinar o fluxo total. Sabemos que o mesmo é dado por
Portanto, como , temos
Analisando todas as alternativas, vemos que a alternativa que mais se aproxima de nossa resposta é a letra .