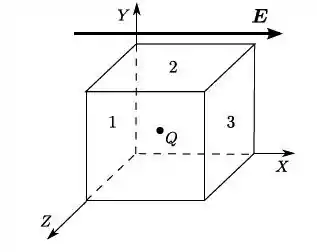
Numa região do espaço de interesse, existe um campo elétrico constante (uniforme e estacionário), na direção e sentido de . Nessa mesma região, temos uma superfície cúbica abstrata, que encerra uma partícula (pontual) de carga localizada no seu centro. Três das faces do cubo estão assinaladas na figura: as faces e são paralelas ao plano , ao passo que a face é paralela ao plano . Em relação ao fluxo (, , ) do campo elétrico através de cada uma dessas faces (com orientação do vetor normal para fora, como usual), qual das alternativas abaixo é a correta?
Passo 1
Como o fluxo de campo elétrico é dado pela seguinte fórmula:
Podemos ver que, quando o vetor aponta no mesmo sentido do campo temos fluxo positivo, ao passo que temos fluxo negativo quando eles apontam em sentidos opostos.
Passo 2
Portanto em função disto temos que a carga faz fluxo positivo em todas as três superfícies e com a mesma intensidade, por conta da simetria.
Já o campo externo tem um fluxo que depende da superfície. O vetor área da superfície é perpendicular à ele, portanto o fluxo é zero.
Passo 3
Na superfície ele é negativo, pois tem sentidos opostos:
Passo 4
E na superfície ele é positivo, por terem mesmos sentidos:
Portanto, como os fluxos de são todos iguais e positivos, podemos afirmar seguramente que:
Resposta
Letra e