UFJF – Física 3 – AV1 – 2014.1 – Questão 3a
Uma bola esférica de cobre tem raio e se encontra em posição concêntrica dentro de uma cavidade esférica de cobre de raio intermo . Na esfera interna existe uma elétrica .
(a) Use a lei de Gauss para calcular o campo elétrico na região .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma bola esférica de cobre de raio que possui carga dentro de outra “bola” de raio .
A questão nos pede para calcularmos o campo elétrico na região entre as duas esferas utilizando a Lei de Gauss.
Lembrando que a Lei de Gauss é dada por:
Onde é o diferencial de área e é a constante de permissividade elétrica no vácuo.
E aí? Bora responder?
Passo 2
Bom... vamos considerar a seguinte figura:
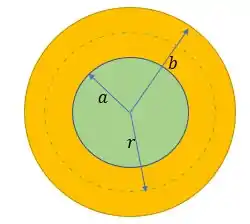
Em que a região pontilhada de raio é a gaussiana.
Considerando a gaussiana da figura acima, determina-se que o campo elétrico em função da distância utilizando a Lei de Gauss:
Passo 3
Dessa forma, substituindo na Lei de Gauss, temos:
A integral que se trata acima é nada mais do que a área da gaussiana. Assim, a área dessa esfera é . Logo:
Por fim, substituindo os valores informados no enunciado, temos:
Entendeu direitinho?? Então responde aí😉
