Unicamp – Física 3 2020.2 – P1 – Questão 1
Esse enunciado utiliza os dados de matrícula dos alunos, mas nós do RA adaptamos para você!
Para calcular o campo elétrico de três distribuições de carga distintas, um aluno utiliza as superfícies gaussianas (em azul) contidas nas Figuras 1 a 3.
Para todas as geometrias acima, considere que a carga está uniformemente distribuída (todas as distribuições possuem densidade volumétrica de carga constante). Calculando o fluxo do campo elétrico que atravessa cada superfície gaussiana em função da distância o aluno montou os seguintes gráficos: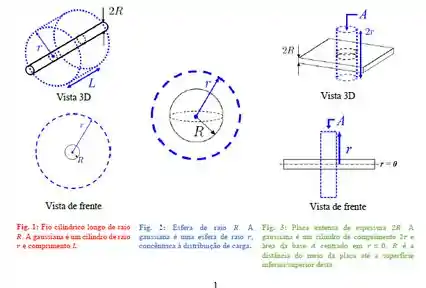 
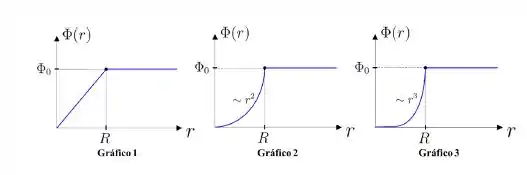
Com base nestas informações:
a) Associe cada gráfico a sua respectiva geometria de carga (cilíndrica, esférica, planar).
Sendo e .
b) Calcule o módulo do campo elétrico na superfície da distribuição de carga.
c) Qual o valor de ?
d) (1.0) Qual seria a nova forma do fluxo se ao invés de uma densidade de carga constante tivéssemos a densidade variável dada por:
Passo 1
Fala galera, tudo bem? Vou ajudar você aqui!
Letra (a):
Temos que o fluxo é o produto do campo pela área, certo?
E já estamos sabemos que o campo elétrico produzido por uma esfera quando cai com , então temos que nesse caso o fluxo é:
Então o fluxo aqui é linear com .
Já o campo fora de um cilindro cai com , então pensando da mesma forma, o fluxo vai com e a simetria linear com .
Assim a ordem dos gráficos é: esférica, cilíndrica, planar.
Passo 2
Letra (b):
Pela lei de Gauss temos:
A carga interna é:
E temos que na superfície esférica a área gaussiana é , daí temos:
Passo 3
Letra (c):
E de novo da lei de Gauss temos:
Daí é:
Passo 4
Letra (d):
Agora a densidade não é mais constante, e precisamos calcular novamente a carga interna. Daí temos:
E o novo fluxo é: