Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fluxo de Campo Elétrico

Ver Teoria
Exercício 3124567891011121314151617181920212223242526272829303132333435363738394041424344454647

Enunciado

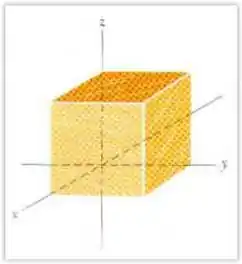
Em todos os pontos da superfície do cubo da figura, o campo elétrico é paralelo ao eixo z , O cubo tem 3 m de aresta. Na face superior do cubo, E → = - 34 k ^ N C , na face inferior, E → = 20 k ^ N C . Determine a carga existente no interior do cubo.

Passo 1

O campo elétrico possui a direção do eixo z . Então, o fluxo em todas as faces que não sejam nem a face de cima e nem a face inferior é nulo. Pois nas demais faces os campos elétricos são ortogonais aos vetores normais. Logo:

Φ E S Q U E R D A = Φ D I R E I T A = Φ F R E N T E = Φ T R A S = 0

Passo 2

Então o nosso problema se resume a calcular o fluxo na parte de cima e na parte de baixo. Na parte superior o campo vale:

E → = - 34 k ^ N C

O vetor normal nessa face possui sentido oposto:

n ^ S U P E R I O R = k ^

Então, o fluxo vale o produto entre a área e o campo com o sinal negativo:

Φ S U P E R I O R = - 34 k ^ . 3 2 k ^ = - 306   k ^ ⋅ k ^ = - 306 N . m 2 C

Passo 3

Fazemos a mesma coisa na face de baixo, mas aí o valor do campo muda:

E → = 20 k ^ N C

O vetor normal nessa face possui sentido oposto ao campo também:

n ^ I N F E R I O R = - k ^

Então, o fluxo vale o produto entre a área e o campo com o sinal negativo:

Φ I N F E R I O R = 20 k ^ . - 3 2 k ^ = - 180 k ^ ⋅ k ^ = - 180 N . m 2 C

Passo 4

Calcular o fluxo total:

Φ T O T A L = - 306 - 180 = - 486 N . m 2 C  

Passo 5

Aplicar a lei de Gauss:

Φ T O T A L = - 486 N . m 2 C = Q I N T ϵ 0 →

Q i n t = - 486.8,85.10 - 12 = - 4301.10 - 12 C = - 4,3   n C

Resposta

Q i n t = - 4,3   n C

Exercícios de Livros Relacionados

15.8E As duas pequenas esferas metálicas vistas na Figura 15.16, de mesmo raio, estão suspensas por fios finos de náilon.Mostre que θ ' = θ . (B) Imagine que um fino fio condutor faça contato simultân
O fluxo de campo elétrico em cada face de um dado tem um valor absoluto, em unidades de 10 3 N · m 2 / C , igual ao número N de pontos da face ( 1 ⩽ N ⩽ 6 ). O fluxo é para dentro se N for ímpar e par
Um cubo possui arestas com comprimento L e é colocado com um dos vértices na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, porém é dado por E → = - B i ^ + C j ^ - D k ^ , onde
O campo elétrico E → 1 em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico E → 2 também é uni
Uma superfície plana quadrada com lado igual a L é descrita pelas equações a Faça um desenho do quadrado e mostre os eixo x ,y e z . b Calcule o fluxo elétrico através do quadrado produzido por uma ca