Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fluxo de Campo Elétrico

Ver Teoria
Exercício 1912345678910111213141516171820212223242526272829303132333435363738394041424344454647

Enunciado

A figura abaixo mostra algumas linhas de campo elétrico gerado por duas placas condutoras planas e paralelas com uma área A muito maior que a separação entre elas, carregadas com densidade uniforme de cargas σ , e no seu interior uma esfera condutora neutra. S 1 e S 2 são duas superfícies fechadas que envolvem completamente uma das placas e a esfera respectivamente. O fluxo elétrico sobre as superfícies S 1 e S 2 são, respectivamente:

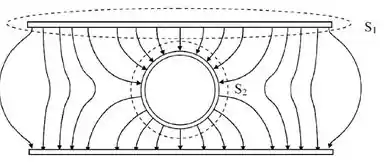
  1. Φ E = 0 e Φ E = ϵ 0 σ / A
  2. Φ E = ϵ 0 σ / A e Φ E = 0
  3. Φ E = A σ / ϵ 0 e Φ E = 0
  4. Φ E = 2 A σ / ϵ 0 e Φ E = ϵ 0 σ / A
  5. Φ E = 2 A σ ϵ 0 e Φ E = 2 A σ / ϵ 0

Passo 1

Pela lei de Gauss, temos que o fluxo do campo elétrico ao longo de uma superfície fechada é dado por

Φ E = Q d e n t r o ϵ 0

Onde Q d e n t r o é a carga total dentro da superfície fechada.

A superfície S 1 contém uma das placas com densidade superficial de carga σ . Como ela tem área A a carga total é dada por

Q d e n t r o 1 = A σ

De forma que

Φ E S 1 = A σ ϵ 0

A superfície S 2 contém a esfera neutra, ou seja, a carga total no interior da superfície S 2 é nula, assim

Φ E S 2 = 0

Resposta

(C)

Exercícios de Livros Relacionados

15.8E As duas pequenas esferas metálicas vistas na Figura 15.16, de mesmo raio, estão suspensas por fios finos de náilon.Mostre que θ ' = θ . (B) Imagine que um fino fio condutor faça contato simultân
O fluxo de campo elétrico em cada face de um dado tem um valor absoluto, em unidades de 10 3 N · m 2 / C , igual ao número N de pontos da face ( 1 ⩽ N ⩽ 6 ). O fluxo é para dentro se N for ímpar e par
Um cubo possui arestas com comprimento L e é colocado com um dos vértices na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, porém é dado por E → = - B i ^ + C j ^ - D k ^ , onde
O campo elétrico E → 1 em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico E → 2 também é uni
Uma superfície plana quadrada com lado igual a L é descrita pelas equações a Faça um desenho do quadrado e mostre os eixo x ,y e z . b Calcule o fluxo elétrico através do quadrado produzido por uma ca