UFRJ – Física 3 2020.2 – P2 – Questão 9
Em uma região do espaço existe um campo elétrico , se , e se , onde . Considere um cilindro imaginário de de comprimento e de raio da base, com centro na origem e eixo sobre o eixo . Qual é a carga total no interior do cilindro?
Passo 1
Fala galera, tudo bem?
Aqui vou usar a lei de Gauss: supondo um cilindro de raio igual a e comprimento , fluxo elétrico é:
Onde é o ângulo entre o vetor normal à área e o campo . O campo é ao longo do eixo , então as únicas áreas que vão contabilizar para o fluxo são da base e do topo do cilindro, saca só:
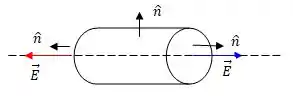Então para o fluxo temos:
Beleza até aqui?
Passo 2
Agora usando a lei de Gauss temos:
Os dados são:
Agora é só substituir:
Analisando as alternativas, a correta é a (d).
Resposta
Exercícios de Livros Relacionados
15.8E As duas pequenas esferas metálicas vistas na Figura 15.16, de mesmo raio, estão suspensas por fios finos de náilon.Mostre que θ ' = θ . (B) Imagine que um fino fio condutor faça contato simultân
O fluxo de campo elétrico em cada face de um dado tem um valor absoluto, em unidades de 10 3 N · m 2 / C , igual ao número N de pontos da face ( 1 ⩽ N ⩽ 6 ). O fluxo é para dentro se N for ímpar e par
Um cubo possui arestas com comprimento L e é colocado com um dos vértices na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, porém é dado por E → = - B i ^ + C j ^ - D k ^ , onde
O campo elétrico E → 1 em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico E → 2 também é uni
Uma superfície plana quadrada com lado igual a L é descrita pelas equações a Faça um desenho do quadrado e mostre os eixo x ,y e z . b Calcule o fluxo elétrico através do quadrado produzido por uma ca