Considere a figura abaixo em que o sólido é um cubo de aresta 1. O campo elétrico é uniforme e tem direção e sentido do eixo com módulo .
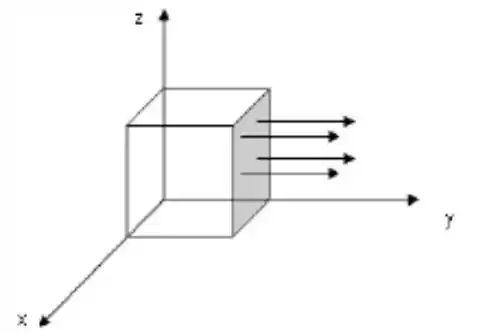
Determine o fluxo elétrico através do cubo, em unidades do SI.
Dado:
Passo 1
Pra essa questão precisamos pensar no que é o fluxo elétrico, pra isso, vamos definir primeiro o que é um fluxo (matematicamente falando, por que sei que todos adoram rsrs). Bom, o fluxo de um campo vetorial nada mais é do que o número de linhas desse campo que atravessam um sólido, então, para o caso em que o campo vetorial é o campo elétrico, temos o fluxo elétrico. Tudo beleza?!
Agora, vamos pensar no seguinte, o campo elétrico segue a direção e sentido do eixo , então a face mais escura na figura e a face oposta a essa possuem o mesmo campo elétrico em módulo porém em sentidos contrários, então podemos calcular o fluxo em cada uma destas faces. Antes de calcular o fluxo, vamos escrever o campo elétrico dado como um vetor, para a face a direita, temos (lembre-se das bases canônicas)
E para a face a esquerda, temos
Agora, podemos calcular o fluxo, temos que
Para a face a esquerda, temos
é dado e , então
Para a outra face, temos
Como as outras faces não possuem um campo elétrico agindo sobre elas, o fluxo nelas é nulo. Então, podemos agora calcular o fluxo total
Ou seja, o fluxo elétrico é nulo.
Resposta
O fluxo elétrico é nulo.