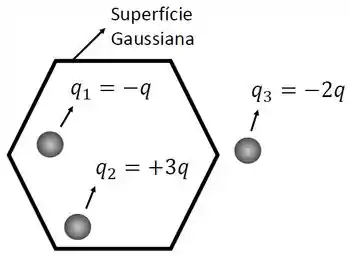
As cargas e encontram-se no interior da superfície gaussiana representada pelo hexágono da figura abaixo, enquanto a carga encontra-se no exterior da superfície gaussiana. Seja o fluxo de campo elétrico total através da superfície Gaussiana e , e representam os fluxos de campo elétrico gerados individualmente pelas cargas , e , respectivamente. A respeito dos fluxos de campo elétrico definidos, a alternativa CORRETA é:
(a) e
(b) e
(c) e
(d) e
(e) e
Passo 1
Primeiramente, vamos relembrar a lei de Gauss na forma integral.
Esta lei diz que o fluxo de um campo elétrico por uma superfície fechada genérica é dada por
Na equação anterior, é a carga elétrica líquida dentro da superfície que cria o campo elétrico . Esta superfície recebe o nome de superfície gaussiana. A grande sacada dessa lei que o fluxo não depende da superfície gaussiana, só da carga interna à superfície.Assim, para responder nossa questão, calcularemos o fluxo de cada carga pela superfície dada no enunciado e o fluxo total pela superfície. Vamos para o próximo passo.
Passo 2
Vamos calcular o fluxo de cada carga e o fluxo total pela superfície gaussiana.
A carga está dentro da superfície gaussiana. Assim, o fluxo devido à carga é
A carga também está dentro da superfície gaussiana. Assim, o fluxo devido à carga é
A carga está fora da superfície gaussiana. Assim, o fluxo devido à carga é
O fluxo total (devido a todas as cargas) pela superfície é a soma de todos os fluxos. Assim,
Analisando todos os itens, vemos que a resposta correta é a letra .