(a)
(b)
(c)
(d)
(e)
Passo 1
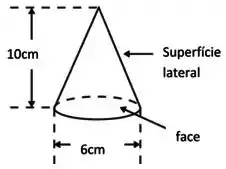
O cone é uma superfície fechada e cada linha do campo uniforme que entra no cone, sai dele. Então, o fluxo elétrico é zero.
Mas esse fluxo é a soma do fluxo na face com o fluxo na superfície lateral. Então:
A gente vai calcular primeiro o fluxo da face, por ser mais fácil.
Passo 2
O campo aponta verticalmente para cima, está entrando pela face. Por isso, o fluxo da face é negativo. Como o campo é ortogonal à base desse cilindro, é só a gente multiplicar a área da face pelo campo:
Por isso:
Resposta
Letra (a)
Exercícios de Livros Relacionados
15.8E As duas pequenas esferas metálicas vistas na Figura 15.16, de mesmo raio, estão suspensas por fios finos de náilon.Mostre que θ ' = θ . (B) Imagine que um fino fio condutor faça contato simultân
O fluxo de campo elétrico em cada face de um dado tem um valor absoluto, em unidades de 10 3 N · m 2 / C , igual ao número N de pontos da face ( 1 ⩽ N ⩽ 6 ). O fluxo é para dentro se N for ímpar e par
Um cubo possui arestas com comprimento L e é colocado com um dos vértices na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, porém é dado por E → = - B i ^ + C j ^ - D k ^ , onde
O campo elétrico E → 1 em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico E → 2 também é uni
Uma superfície plana quadrada com lado igual a L é descrita pelas equações a Faça um desenho do quadrado e mostre os eixo x ,y e z . b Calcule o fluxo elétrico através do quadrado produzido por uma ca