Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fluxo de Campo Elétrico

Ver Teoria
Exercício 3012345678910111213141516171819202122232425262728293132333435363738394041424344454647

Enunciado

A figura abaixo mostra os planos infinitos I e I I feitos de material não condutor, eletrificados com densidades superficiais de carga σ I e σ I I , respectivamente.

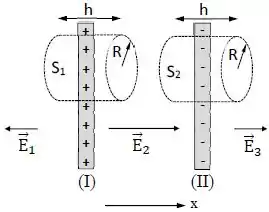
O campo elétrico à esquerda é E 1 = - E s i ^ , no centro é E 2 = 3 E s i ^ e à direita é E 3 = E s i ^ . Além disso, estão indicadas duas superfícies gaussianas cilíndricas, S 1 e S 2 , de altura h e raio R , cujos eixos são perpendiculares aos planos de carga.

Sejam Φ i o fluxo através da superfície S i i = 1,2 , e σ X a densidade superficial de carga no plano X X = I , I I .

Os valores de Φ i e σ X são dados por:

a Φ 1 = 4 π R 2 E s , Φ 2 = 4 π R 2 E s , σ I = 4 ϵ 0 E s , σ I I = - 2 ϵ 0 E s .

b Φ 1 = 3 π R 2 E s , Φ 2 = - π R 2 E s , σ I = 3 ϵ 0 E s , σ I I = - ϵ 0 E s .

c Φ 1 = 4 π R 2 E s , Φ 2 = - 2 π R 2 E s , σ I = 4 ϵ 0 E s , σ I I = - 2 ϵ 0 E s .

d Φ 1 = - 2 π R 2 E s , Φ 2 = 2 π R 2 E s , σ I = 2 ϵ 0 E s , σ I I = - 2 ϵ 0 E s .

e Φ 1 = - 4 π R 2 E s , Φ 2 = - 2 π R 2 E s , σ I = 3 ϵ 0 E s , σ I I = - ϵ 0 E s .

Passo 1

Vamos analisar uma superfície por vez, beleza?

Na superfície S 1 , as linhas dos campos elétricos E 1 →   e   E 2 → atravessam apenas as bases do cilindro, passando paralelamente à superfície lateral do mesmo.

Dessa forma, como ambos os campos estão saindo da superfície S 1 , por definição, o fluxo elétrico total será dado por:

Φ 1 = E 1 A + E 2 A = E s + 3 E s π R 2

Φ 1 = 4 π R 2 E s

Lembrando: Quando as linhas de campo saem de uma superfície, o fluxo é considerado positivo. Quando as linhas de campo entram em uma superfície, o fluxo é considerado negativo.

Passo 2

De acordo com a Lei de Gauss, o fluxo elétrico através de S 1 é dado por:

Φ 1 = q i n t ϵ 0

Dessa forma, igualando com a expressão que encontramos no Passo 1, teremos:

q i n t ϵ 0 = 4 π R 2 E s

Por definição, a carga de uma superfície está associada com a densidade superficial de carga através da equação:

Q = σ A

Logo:

σ 1 A ϵ 0 = 4 π R 2 E s

π R 2 σ 1 ϵ 0 = 4 π R 2 E s

σ 1 = 4 ϵ 0 E s

Passo 3

Agora vamos realizar o mesmo raciocínio para a superfície S 2 .

Aqui, o campo elétrico E 2 → entra na superfície, enquanto o campo elétrico E 3 → sai da superfície, logo, o fluxo elétrico total será:

Φ 2 = - E 2 A + E 3 A = - 3 E s + E s π R 2

Φ 2 = - 2 E s π R 2

Passo 4

Aplicando a Lei de Gauss à S 2 , teremos:

Φ 2 = q i n t ϵ 0 = π R 2 σ 2 ϵ 0

π R 2 σ 2 ϵ 0 = - 2 E s π R 2

σ 2 = - 2 ϵ 0 E s

Passo 5

Resumindo:

Φ 1 = 4 π R 2 E s

Φ 2 = - 2 E s π R 2

σ 1 = 4 ϵ 0 E s

σ 2 = - 2 ϵ 0 E s

A resposta certa é a letra c .

Resposta

c Φ 1 = 4 π R 2 E s , Φ 2 = - 2 π R 2 E s , σ I = 4 ϵ 0 E s , σ I I = - 2 ϵ 0 E s .

Exercícios de Livros Relacionados

15.8E As duas pequenas esferas metálicas vistas na Figura 15.16, de mesmo raio, estão suspensas por fios finos de náilon.Mostre que θ ' = θ . (B) Imagine que um fino fio condutor faça contato simultân
O fluxo de campo elétrico em cada face de um dado tem um valor absoluto, em unidades de 10 3 N · m 2 / C , igual ao número N de pontos da face ( 1 ⩽ N ⩽ 6 ). O fluxo é para dentro se N for ímpar e par
Um cubo possui arestas com comprimento L e é colocado com um dos vértices na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, porém é dado por E → = - B i ^ + C j ^ - D k ^ , onde
O campo elétrico E → 1 em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico E → 2 também é uni
Uma superfície plana quadrada com lado igual a L é descrita pelas equações a Faça um desenho do quadrado e mostre os eixo x ,y e z . b Calcule o fluxo elétrico através do quadrado produzido por uma ca