UFJF – Física 3 – AV1 – 2014.1 – Questão 3b
Uma bola esférica de cobre tem raio e se encontra em posição concêntrica dentro de uma cavidade esférica de cobre de raio intermo . Na esfera interna existe uma elétrica .
(b) Calcule o trabalho necessário para transportar uma carga da parede da cavidade até a bola interna.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma bola esférica de cobre de raio que possui carga dentro de outra “bola” de raio .
A questão nos pede para calcularmos o trabalho envolvido para trazer uma carga de da parede da cavidade até a bola interna.
Para isso, temos que saber que o trabalho é dado por:
E aí? Bora responder?
Passo 2
Bom... vamos considerar a seguinte figura:
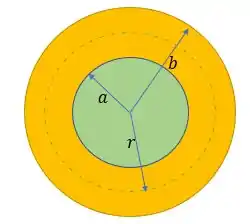
Em que é o raio da gaussiana.
Pela questão anterior, vimos que o campo elétrico entre as esferas é de:
Concorda comigo que para trazer a carga de da parede da cavidade até a bola interna é necessário ter a atuação desse campo que descobrimos?
Pois é!! Então basta aplicarmos na fórmula do Passo1!!
Passo 3
Dessa forma, substituindo, temos:
Entendeu direitinho?? Então responde aí😉
