Uma esfera isolante de raio está uniformemente carregada com uma carga total . Desenhamos então uma superfície quadrada , de lado , que corta a esfera ao meio, como mostrado na figura abaixo.
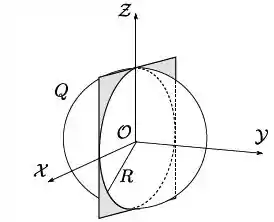
Essa superfície é desenhada de forma a coincidir com o plano de um sistema de coordenadas com origem no centro da esfera, e a sua normal é escolhida ao longo de positivo.
Dessa forma, qual é o fluxo de campo elétrico através de ?
Passo 1
O fluxo de campo elétrico através da superfície é dado por:
Agora, pensa aqui comigo. O fluxo passando por aquele quadrado pode ser dividido em dois fluxos: um causado por uma metade da esfera e outro causado pela outra metade.
O que acontece é que os dois fluxos são iguais em módulo, por simetria, e têm sinais opostos. Porque uma metade gera campo na direção -y e outra gera na direção +y, assim, o fluxo total é nulo.
Ou seja:
Logo: