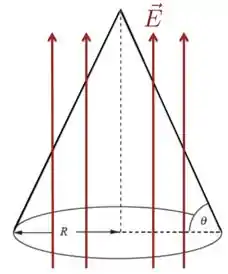
Um cone circular reto imaginário, como mostrado na Figura abaixo, com ângulo de base e raio da base está em uma região livre de cargas que tem um campo elétrico uniforme , cujas linhas de campo são verticais e paralelas ao eixo do cone, como na figura. Qual o fluxo do campo elétrico pela área lateral desse cone?
Passo 1
Bem, pra calcular o fluxo do campo elétrico temos que fazer a seguinte integral
Só que calcular isso é osso, por que o campo elétrico faz um certo ângulo com essa superfície lateral o que é chatinho de fazer.... se fosse pra calcular pra base desse cone seria moleza xD
Passo 2
Mas existe um negócio que pode nos salvar! Esse negócio é a lei de Gauss!
O que a lei de Gauss diz? Como dentro desse cone não há carga, o fluxo no cone todo (que é uma superfície fechada) é nulo, ou seja
Só que o fluxo do campo elétrico dentro do cone pode ser dividido em duas partes
Como
Aí sim!!! O fluxo do campo elétrico na base é bem mais tranquilo de calcular!
Passo 3
Agora vamos calcular .
Como temos uma superfície fechada temos que orientar a normal da superfície apontando para fora do volume, assim, na base do cone a normal aponta para baixo, ou seja
Assim
Passo 4
Assim, finalmente temos que