Uma partícula com carga encontra-se na origem do sistema de coordenadas mostrado na figura
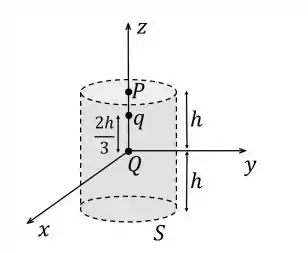
- Escreve a expressão do campo elétrico , devindo à carga , o ponto do eixo , localizado a uma altura do plano
- Qual carga , colcoada em anula o fluxo do campo elétrico através da superfície cilíndrica fechada que contém o ponto ?
- Qual carga , colocada em , anula o campo elétrico no ponto
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
Temos duas cargas partículas dentro de um cilindro, uma e outra . Ok, nosso trabalho então é saber algumas coisas sobre ela. Bom, quais são elas? Se eu pegar um ponto na superfície, qual seria o campo elétrico dele divido à carga ? Qual carga colocada dentro do cilindro anularia o campo elétrico na superfície? E qual carga eu coloco eu cancelo o campo elétrico no ponto ? E existem muitas mais, como qual seria o potencial elétrico? Existem muitas coisas mais para sabermos se quiséssemos. Tente, e verá como o eletromagnetismo é lindo!
Então bora lá ver como calcular o campo elétrico na superfície de um objetivo com carga no eixo de simetria?
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Para a)
Veja que nós temos uma carga no centro, e queremos saber o campo elétrico na superfície. Bom, podemos aplicar a lei de Gauss para calcularmos o fluxo elétrico a superfície, certo? Sabemos que o fluxo elétrico pela lei de Gauss é:
Considerando o campo elétrico constante:
Como é a nossa área? Bom, é um cilindro, e a nossa distâancia do ponto à carga é h, certo? Então sendo a distância, assim . Logo:
E achamos o campo elétrico ao longo do eixo z. Caso queira vetorialmente, teríamos:
Passo 3
Para b)
Aqui é uma parte mais conceitual. Veja!
Para cancelar o fluxo do campo elétrico, sabemos pela lei de Gauss que o fluxo é nulo se a carga interna total também for nula. Então, bom... Temos que ter uma carga interna nula, e temos , para que seja então a carga interna deve ser:
Passo 4
Para c)
Aqui queremos saber como que podemos cancelar o campo elétrico com uma carga a uma distancia dele. Assim, queremos que . Como podemos fazer isso? Bom, podemos usar o principio da superposição, isto é:
Sendo e os campos que vamos ver que resultam o total. Bom, como queremos saber qual carga qeue vai anular o campo, então temos que fazer:
Mas qual é o campo elétrico pontual gerado pela carga ? Bom, o campo elétrico em devido à carga pela mesma lei de Gauss que usamos no item a é:
Usando novamente que e que a distâancia do ponto P a carga é , assim . Logo:
Assim retornando ao nosso campo total, temos:
Queremos saber o valor , então vamos iniciar o processo de isolar ele.
Passando pro outro lado:
Multiplicando ambos os lados por , temos:
Isolando , temos:
E assim achamos qual valor de temos que ter para cancelar o campo elétrico no ponto
Resposta
Para a)
Para b)
Para c)