Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial no R³

Ver Teoria
Exercício 371234567891011121314151617181920212223242526272829303132333435363839

Enunciado

Seja C a interseção do cilindro x 2 + y 2 = 4 com o semiplano y + z = 0 , y ≥ 0 , percorrida de modo que sua projeção no plano x y tenha sentido anti-horário e seja F → x , y , z = x 4 i → + y 4 j → + z 4 k → . Calcule a integral

∫ C F → ∙ d r →

Passo 1

Bem, sempre resolvemos uma integral de linha seguindo alguns passinhos lindo:

  1. Parametrizar a curva C que estamos trabalhando
  2. Substituir os termos do campo vetorial F → x ,   y pelos termos da parametrização
  3. Encontrar o termo d r →

Então vem comigo nessa aventura! :D

Passo 2

Precisamos conseguir parametrizar a curva C , Mas quem é mesmo essa curva?

Se desenharmos no espaço esse cilindro x 2 + y 2 = 4

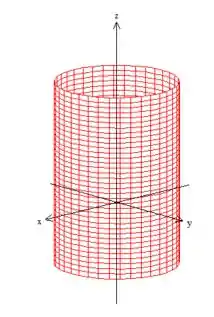
cortado pelo semi plano y + z = 0 ...

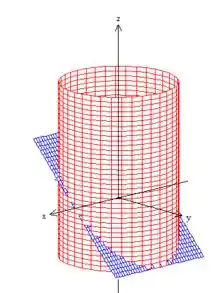
Eis a nossa curva onde o y ≥ 0 :

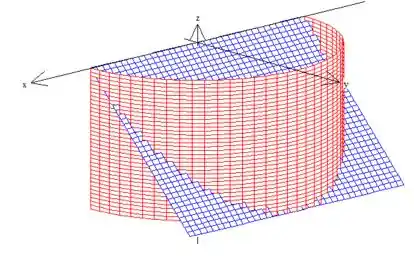
Como estamos em um cilindro, podemos parametrizar o cilindro direto

x 2 + y 2 = 4

Vamos ter

x = 2 cos ⁡ θ

y = 2 sen ⁡ θ

Ele disse que y > 0 isso nos diz que

2 sen ⁡ θ > 0

sen ⁡ θ > 0

Então

θ ∈ 0 , π

Falta a componente z , mas temos uma relação entre y e z

z + y = 0

Então

z = - 2 sen ⁡ θ

z = - 2 sen ⁡ θ

Vamos ter

σ θ = 2 cos ⁡ θ , 2 sen ⁡ θ , - 2 sen ⁡ θ

Como estamos saindo do eixo x e dando uma meia volta:

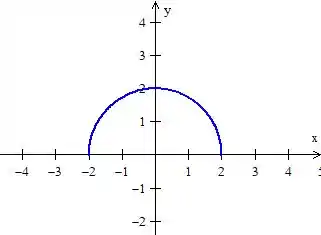
Então:

θ ∈ 0 , π

Passo 3

Pow, nos falta encontrar d r → , porém

d r → = σ ' θ d θ

Agora calculamos σ ' θ

σ ' θ = ∂ ∂ θ 2 cos ⁡ θ , ∂ ∂ θ 2 sen ⁡ θ , ∂ ∂ θ - 2 sen ⁡ θ = - 2 sen ⁡ θ , 2 cos ⁡ θ , - 2 cos ⁡ θ

logo

d r → = - 2 sen ⁡ θ , 2 cos ⁡ θ , - 2 cos ⁡ θ d θ

Uma coisa que temos que ficar atentos na integral de linha é o sentido do cara!

Ele disse que o sentido é anti-horário da projeção no plano x y , isso já é a orientação normal que temos, e estamos rodando no sentido anti-horário. Se não tivéssemos, bastava trocar o sinal desse vetor, sacou?

Passo 4

Vamos, então, substituir todos os ingredientes até aqui encontrados na integral.

∫ 0 π 2 cos ⁡ θ 4 , 2 sen ⁡ θ 4 , - 2 sen ⁡ θ 4 ∙ - 2 sen ⁡ θ , 2 cos ⁡ θ , - 2 cos ⁡ θ d θ

= ∫ 0 π 16 cos 4 ⁡ θ , 16 sen 4 ⁡ θ , 16 sen 4 ⁡ θ ∙ - 2 sen ⁡ θ , 2 cos ⁡ θ , - 2 cos ⁡ θ d θ

= ∫ 0 π - 32 cos 4 �� θ sen ⁡ θ + 32 sen 4 ⁡ θ cos ⁡ θ - 32 sen 4 ⁡ θ cos ⁡ θ d θ

= ∫ 0 π - 32 cos 4 ⁡ θ sen ⁡ θ d θ

= - 32 ∫ 0 π cos 4 ⁡ θ sen ⁡ θ d θ

Vamos resolver essa integral separada

Passo 5

∫ cos 4 ⁡ θ sen ⁡ θ d θ

Vamos fazer

u = cos ⁡ θ

Então

d u = - sen ⁡ θ d θ

A integral vai ficar

∫ cos 4 ⁡ θ sen ⁡ θ d θ = - ∫ u 4 d u

Resolvendo a integral vamos ter

- ∫ u 4 d u = - u 5 5

Voltando para θ

- u 5 5 = - cos 5 ⁡ θ 5

Passo 6

Voltando para nossa integral

= - 32 ∫ 0 π cos 4 ⁡ θ sen ⁡ θ d θ

Vamos ter

= - 32 - cos 5 ⁡ θ 5 θ = 0 π

= - 32 - cos 5 ⁡ π 5 - - cos 5 ⁡ 0 5

= - 32 - - 1 5 5 - - 1 5 5

= - 32 - - 1 5 - - 1 5

= - 32 1 5 + 1 5

= - 32 2 5

= - 64 5

Resposta

- 64 5

Exercícios de Livros Relacionados

Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:24. ∫ C y d x + z d y - x y d z , onde C é dada por y = s e nx ; z = 4 ; x ∈ [ 0,2 π ] .
Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:22. ∫ C d x + d y + d z , onde C é a intersecção das superfícies y + z = 5 e z = 4 - x 2 do ponto A ( 2 ,5 ,0 ) ao ponto B ( - 2 ,5 ,0 )
Calcule ∫ γ d x + x y d y + zd z , onde γ é a interseção de x 2 + y 2 + z 2 = 2 ,x ≥ 0 ,y ≥ 0 e z ≥ 0 , com o plano y = x ; o sentido do percurso é do ponto 0,0 , 2 para 1,1 , 0 .
Calcule a integral de linha ∫ C F → ∙ d r → , onde C é dada pela função vetorial r → t . F → x ,y = x + yi ^ + y - z j ^ + z 2k ^ r → t = t 2i ^ + t 3j ^ + t 2k ^ , 0 ≤ t ≤ 1
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = y 2 c o s c o szi → + 2 x y c o szj → - x y 2 s e nz k → ,C : r → t = t 2 i →