20) Seja de classe , tal que . Considere o campo . Calcule onde é a curva formada por e .
Passo 1
Bem, eu sei que está muuuito confuso o enunciado e que apareceram vários caras “novos” como e entre outros. Porém o que o problema quer na realidade é uma integral de linha:
Onde a curva é uma curva fechada entre esse pedacinho da função cúbica e essa reta:
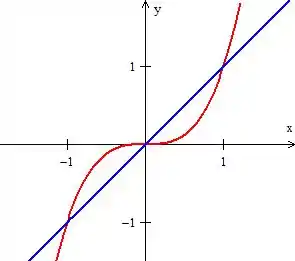
Pow! Então eu te recomendo que você não se preocupe agora com aquelas outras informações dadas agora e que comece a resolvendo a integral de linha normalmente como estamos acostumados até agora:
- Como estamos em uma região fechada, aplicando o nosso amigo “O Teorema de Green” ! Venha comigo! :D
- Que é uma função que leva a (então é uma função escalar de duas variáveis ) e que .
Passo 2
O teorema de Green nada mais é do que essa igualdade mara entre a integral de linha com uma integral dupla:
Mas antes de aplicarmos essa igualdade maravilhosa do Teorema, temos que avalizar as condições de Green, que sempre nos exige:
1º - Uma curva fechada que delimita .
2º - Orientadas positivamente.
3º - Um campo sem singularidades onde estamos trabalhando.
Vamos averiguar?
Passo 3
Sobre uma curva fechada está ok, pois a como já vimos ela é fechada, inclusive foi a nossa inspiração inicial para aplicar o Teorema, certo?
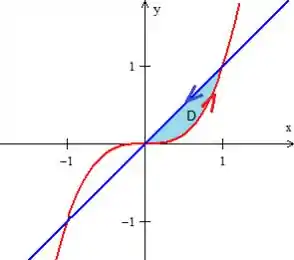
E em relação a ser orientada positivamente também está ok, pois quando um problema não nos diz nada sobre a orientação, adotamos a curva girando no sentido anti-horário... Orientada positivamente, portanto. :D
Campo sem singularidades também está sendo satisfeito, pois o que acontece, o campo é formado das primeiras derivadas de a qual sabemos ser de classe , então também é de classe . Sendo assim, ele não tem nenhum problema, pois se tivesse, ele não seria, saca?
Passo 4
Condições do Teorema sendo satisfeitas, podemos aplicar a igualdade numa boa:
Se queremos essa integral de linha, calculemos a integral dupla e é só correr para o abraço. Porém antes, temos que determinar essas derivadas parciais aí:
Como...
Calculando a primeira derivada parcial...
Então...
E a integral dupla fica sendo:
Passo 5
Agora, utilizemos a última informação:
Cara, se você não se lembra dele, é um operador de derivadas parciais ao qual damos o nome de Operador Laplaciano.
Não estamos interessados no significado físico dessa coisa, mas sim no matemático. E pow, esse operador matematicamente é definido como...
é o operador de derivadas parciais e é esse vetor aqui:
Então é o gradiente dado pelo produto da função escalar pelo operador:
E aplicando o divergente (o produto escalar de vetores), fica...
Como ...
Passo 2
Voltando para a integral dupla...
Para resolver essa integral, devemos descrever a região ...
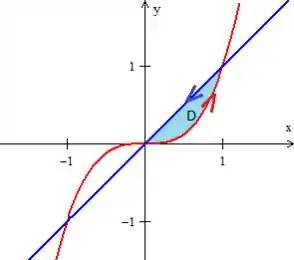
que pode ser feito utilizando o Tipo de classificação:
Substituindo na integral...
Logo, a integral de linha que procurávamos, pelo Teorema de Green é...