Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial no R³

Ver Teoria
Exercício 191234567891011121314151617182021222324252627282930313233343536373839

Enunciado

  1. Calcule o trabalho realizado pela força F → = ( x ,   y ,   z ) para deslocar uma partícula ao longo da curva interseção das superfícies x + z = 5 e z = 4 - y 2 , orientada do ponto 5 ,   - 2 ,   0 a 5 ,   2 ,   0 .

Passo 1

Para acharmos o trabalho de F → devemos fazer a integral de linha de F → ao longo da curva C que é a interseçãodas superfícies (já já vamos ver melhor quem é ):

T r a b a l h o = ∫ C   F → d r →

Encontrar uma solução para uma integral de linha nada mais é do que seguir um passo a passo maroto:

  1. Parametrizar a curva C que estamos trabalhando.
  2. Substituir os termos do campo vetorial F → x ,   y ,   z pelos termos da parametrização.
  3. Encontrar o termo d r → .

Então vem comigo nessa aventura! :D

Passo 2

Vamos então parametrizar a curva C , mas por falar nisso, quem é a curva C ?

Como nos pediu o exercício, a curva é dado pela interseção do cilindro parabólico z = 4 - y 2

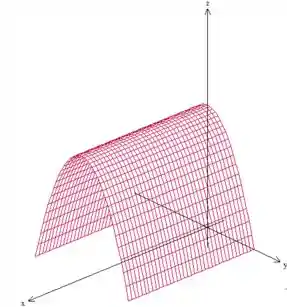
com esse plano paralelo ao eixo y , x + z = 5 , bonitinho aqui:

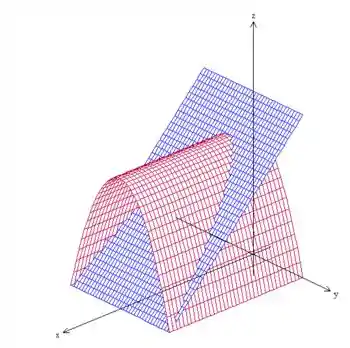
Sacou? :D

Passo 3

Pow! Resolver uma interseção em Matemática é resolver o sistema com as equações das superfícies envolvidas:

x + z = 5 z = 4 - y 2

Isolando z na primeira...

z = 5 - x

e substituindo na segunda:

z = 4 - y 2           →               5 - x = 4 - y 2           →

- x = 4 - 5 - y 2         →         -   x = - 1 - y 2       - 1   →        

x = 1 + y 2

Essa equação nos representa essa parábola ao redor de x aqui oh:

Passo 4

Bem! Se estamos trabalhando com uma equação explícita podemos pensar em uma parametrização também explícita, onde se chamarmos...

y = t

x = 1 + y 2     →               x = 1 + t 2

enquanto z ...

z = 4 - y 2     →               x = 4 - t 2

Logo, a parametrização arrumada bonitinha é:

γ t = 1 + t 2   ,   t   ,   4 - t 2

Já sabemos que não saímos de uma parametrização sem antes determinar ondo o parâmetro, no caso o t , está variando, e pow, sabemos que t é y e pelo próprio problema estamos saindo do ponto 5 ,   - 2 ,   0 onde y = - 2 e indo até 5 ,   2 ,   0 , y = 2 , logo:

- 2 ≤ t ≤ 2

Passo 5

Precisamos agora encontrar o campo em em termos dos parâmetro:

F → = ( x ,   y ,   z )

Basta trocar tudo que é x por 1 + t 2 , y por t e z vira...

F → = x ,   y ,   z =

F → = 1 + t 2 ,   t   ,   4 - t 2  

Passo 6

Para encontrar o termo d r → , basta sabermos que facilmente o encontramos fazendo:

d r → = γ ' t d t

Como no caso a parametrização foi γ t = 1 + t 2   ,   t   ,   4 - t 2 , derivando cada termo do vetor em relação a t ...

γ t = 1 + t 2   ,   t   ,   4 - t 2             →               γ ' t = 2 t ,   1   ,   - 2 t

Logo...

d r → = 2 t ,   1   ,   - 2 t d t

Passo 7

Voltando para a integral de linha que estamos trabalhando

∫ C   F → x ,   y ,   z d r →

e substituir todos os dados que obtivemos...

∫ C   F → x ,   y ,   z d r → = ∫ - 2 2 1 + t 2 ,   t   ,   4 - t 2   ∙ 2 t ,   1   ,   - 2 t d t

Não se esqueça de realizar esse produto escalar de vetores aí, heim!

∫ - 2 2 1 + t 2 ,   t   ,   4 - t 2   ∙ 2 t ,   1   ,   - 2 t d t = ∫ - 2 2 1 + t 2 2 t +   t +   4 - t 2 - 2 t d t

∫ - 2 2 2 t + 2 t 3 +   t + - 8 t + 2 t 3 d t =

∫ - 2 2 - 5 t + 4 t 3 d t =

- 5 t 2 2 + 4 t 4 4 - 2 2 =

- 5 2 2 2 + 4 2 4 4 - - 5 - 2 2 2 + 4 - 2 4 4 =

- 5 2 2 2 + 4 2 4 4 + 5 2 2 2 - 4 2 4 4 =

0

Resposta

0

Exercícios de Livros Relacionados

Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:24. ∫ C y d x + z d y - x y d z , onde C é dada por y = s e nx ; z = 4 ; x ∈ [ 0,2 π ] .
Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:22. ∫ C d x + d y + d z , onde C é a intersecção das superfícies y + z = 5 e z = 4 - x 2 do ponto A ( 2 ,5 ,0 ) ao ponto B ( - 2 ,5 ,0 )
Calcule ∫ γ d x + x y d y + zd z , onde γ é a interseção de x 2 + y 2 + z 2 = 2 ,x ≥ 0 ,y ≥ 0 e z ≥ 0 , com o plano y = x ; o sentido do percurso é do ponto 0,0 , 2 para 1,1 , 0 .
Calcule a integral de linha ∫ C F → ∙ d r → , onde C é dada pela função vetorial r → t . F → x ,y = x + yi ^ + y - z j ^ + z 2k ^ r → t = t 2i ^ + t 3j ^ + t 2k ^ , 0 ≤ t ≤ 1
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = y 2 c o s c o szi → + 2 x y c o szj → - x y 2 s e nz k → ,C : r → t = t 2 i →