15) Calcule as integrais de linha diretamente e também e também pelo Teorema de Green:
b)
onde é o caminho fechado formado por , e , orientado positivamente.
Passo 1
Antes de tudo, sempre é bom lembrar que uma integral de linha escrita assim
é a mesma coisa que uma escrita assim ...
Onde no caso,
Vamos então primeiro resolver essa integral de linha pelo método direto pedido:
1º - Parametrizando a curva .
2º - Encontrando o termo .
3º - Trabalhando com a função vetorial que está sendo integrada.
Passo 2
Primeiro então devemos parametrizar , que, caso desenhemos utilizando essas três retas (, e ), vamos obter esse triângulo aqui oh:
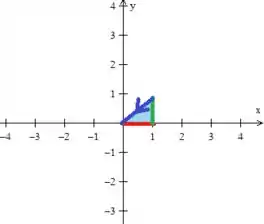
Que gira no sentido anti-horário, pois ela está orientada positivamente, sacou?
Bem, como estamos trabalhando com uma curva composta de outras três
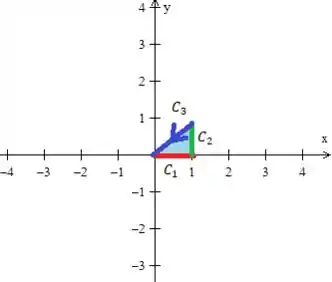
Deveremos parametrizar e calcular uma integral de linha para cada uma delas:
Então vamos nessa?
Passo 3
1º - A curva :
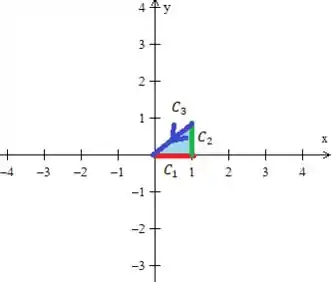
- Como é uma e varia livremente...
- O Termo para essa parametrização é
- O campo nos termos da parametrização...
- Como é uma e varia livremente...
- O Termo para essa parametrização é
- O campo nos termos da parametrização...
- Como agora se trata de ...
- O Termo para essa parametrização é
- O campo nos termos da parametrização...
então
como é e varia de até ...
Com esses três ingredientes, jogando na integral de linha...
Passo 4
2º - A curva :
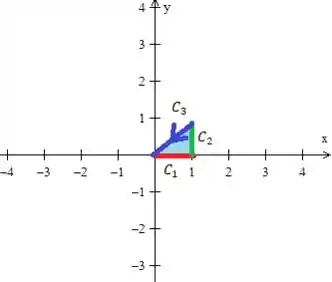
então
como é e varia de até o topo do triangulo que ...
Com esses três ingredientes, jogando na integral de linha...
Passo 5
3º - A curva :
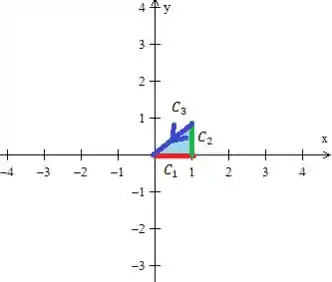
como varia de até ...
Com esses três ingredientes, jogando na integral de linha...
Passo 4
Como
então...
Passo 5
Como o próprio problema pediu, agora vamos resolver a mesma integral utilizando o teorema de Green...
Mas antes de aplicarmos essa igualdade maravilhosa do Teorema, temos que avalizar as condições de Green, que sempre nos exige:
1º - Uma curva fechada delimitando a região .
2º - A curva , orientada positivamente.
3º - Um campo sem singularidades onde estamos trabalhando.
Vamos averiguar?
Passo 6
1º - Precisamos de uma curva fechada e delimitando uma região . Ora, a curva , pelo próprio enunciado, é uma curva fechada é justamente o triângulo:
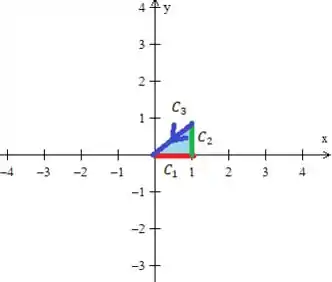
Onde a região é o seu interior.
2º - E mais, ela está orientada positivamente sim!!! Ela gira no sentido anti-horário
3º - O campo que estamos trabalhando...
Não tem um problema em nenhum lugar, o que nos garante que ele já está sem singularidades !
Passo 7
Condições do Teorema sendo satisfeitas, podemos aplicar a igualdade numa boa:
Se queremos a integral de linha, calculemos a integral dupla e beijinho no ombro ;)
Calculando, primeiro, essas derivadas parciais aí do campo...
Logo...
Passo 8
Para resolver a integral dupla necessitamos descrever a região
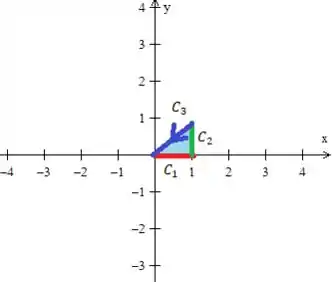
O que pode ser feito utilizando o Tipo como auxílio:
e
Montando a integral...
Logo