Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial no R²

Ver Teoria
Exercício 201234567891011121314151617181921222324252627282930313233343536373839404142434445

Enunciado

  1. Calcule ∫ C   3 x + 2 y d x + 3 x - y d y de ( 0 ,   0 ) a 1 ,   1 , ao longo
  1. do arco da parábola y = x 2 .

Passo 1

Bem, antes do começarmos qualquer coisa, vamos colocar essa integral de linha de uma forma mais elegante.

Como você já pode notar, a integral de linha está assim ∫ C   3 x + 2 y d x + 3 x - y d y , certo? Só que esse formato é apenas outra forma de falar que estamos trabalhando uma integral de linha de um campo de vetores: ∫ C   F → x ,   y d r →

∫ C   3 x + 2 y d x + 3 x - y d y = ∫ C   F → x ,   y d r →

Onde esse F → x ,   y é o vetor...

F → x ,   y = 3 x + 2 y ,   3 x - y  

Se buscamos a solução dessa integral de linha do modo diretão, nada mais justo que seguirmos o passo a passo maroto de resolução desse tipo de integral:

  1. Parametrizar a curva C que estamos trabalhando.
  2. Substituir os termos do campo vetorial F → x ,   y pelos termos da parametrização.
  3. Encontrar o termo d r → .

Então vem comigo nessa aventura! :D

Passo 2

Vamos então parametrizar a curva C , mas por falar nisso, quem é a curva C ?

Bem, pelo próprio enunciado, sabemos que a curva que une esses dois pontos é o pedacinho da parábola y = x 2 :

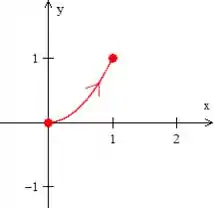
Como temos uma curva como uma função explícita, é bem legal pensarmos em uma parametrização também explícita, onde podemos trocar o

x = t

e imediatamente ganhamos o y ...

y = x 2 = t 2

Arrumando essa parametrização de uma forma mais elegante...

γ t = t ,   t 2

Como t é x e x varia da origem até 1 ...

0 ≤ t ≤ 1

Passo 3

Beleza! Agora devemos prosseguir substituindo no campo vetorial F → x ,   y , esse x e y pelos termos da parametrização:

F → x ,   y = 3 x + 2 y ,   3 x - y         →

Lembrando que x = t e y = t 2 ...

F → γ t = 3 t + 2 t 2 ,   3 t - t 2  

Passo 4

Para encontrar o termo d r → , basta sabermos que facilmente o encontramos fazendo:

d r → = γ ' t d t

Como no caso a parametrização foi γ t = t ,   t 2 , derivando cada termo do vetor em relação a t ...

γ t = t ,   t 2             →               γ ' t = 1 ,   2 t

Logo...

d r → = 1 ,   2 t d t

Passo 5

Voltando para a integral de linha que estamos trabalhando

∫ C   F → x ,   y d r →

e substituir todos os dados que obtivemos...

∫ C   F → x ,   y d r → = ∫ 0 1 3 t + 2 t 2 ,   3 t - t 2   ∙ 1 ,   2 t d t

Não se esqueça de realizar esse produto escalar de vetores aí, heim!

∫ 0 1 3 t + 2 t 2 ,   3 t - t 2   ∙ 1 ,   2 t d t = ∫ 0 1 3 t + 2 t 2 + 2 t 3 t - t 2     d t =

∫ 0 1 3 t + 2 t 2 + 6 t 2 - 2 t 3 d t =

∫ 0 1 3 t + 8 t 2 - 2 t 3 d t

Agora basta que resolva a integral e corra para o abraço!

∫ 0 1 3 t + 8 t 2 - 2 t 3 d t = 3 t 2 2 + 8 t 3 3 - 2 t 4 4 0 1 =

3 2 + 8 3 - 1 2 =

9 + 16 - 3 6 = 11 3

Resposta

a )   11 3

Exercícios de Livros Relacionados

Determine o trabalho realizado pelo campo de força F x ,y = xs e nyi + yj em uma partícula que se move sobre a parábola y = x 2 de - 1 ,1 a 2 ,4 .
Seja F x , y = - yi + xj x 2 + y 2 Mostre que ∂ P / ∂ y = ∂ Q / ∂ x .Mostre que ∫ C F ⋅ d r não é independente do caminho. [Sugestão: calcule ∫ C 1 F ⋅ d r e ∫ C 2 F ⋅ d r onde C 1 e C 2 são as metade
Mostre que um campo de força constante realiza trabalho nulo sobre uma partícula que dá uma única volta completa uniformemente na circunferência x 2 + y 2 = 1 .Isso também é verdadeiro para um campo d
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = 3 + 2 x y 2 i → + 2 x 2 y j → , C é o arco da hipérbole y = 1 x de ( 1,1 ) a
Mostre que a integral de linha é independente e calcule a integral. ∫ C 2 x s e nyd x + ( x 2 cos ⁡ y - 3 y 2 ) d y C é qualquer caminho de ( - 1,0 ) a ( 5,1 )