Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar R³

Ver Teoria
Exercício 181234567891011121314151617192021222324252627282930313233343536373839404142434445464748

Enunciado

  1. Calcule

∫ C   P �� d x + Q   d y + R   d z

Onde:

  1. F → = P ,   Q ,   R = z ,   x ,   y e C é a interseção das superfícies z = x 2 + y 2 e 4 x + 2 y + z = 1 , orientada de modo que sua projeção no plano x y se percorrida uma vez no sentido horário.

Passo 1

Bem, antes do começarmos qualquer coisa, vamos colocar essa integral de linha de uma forma mais elegante.

Como você já pode notar, a integral de linha está assim ∫ C   P   d x + Q   d y + R   d z , certo? Só que esse formato é apenas outra forma de falar que estamos trabalhando uma integral de linha de um campo de vetores: ∫ C   F → x ,   y ,   z d r →

∫ C   P   d x + Q   d y + R   d z = ∫ C   F → x ,   y ,   z d r →

Onde esse F → x ,   y ,   z é o vetor...

F → x ,   y ,   z = z ,   x ,   y

Se buscamos a solução dessa integral de linha do modo diretão, nada mais justo que seguirmos o passo a passo maroto de resolução desse tipo de integral:

  1. Parametrizar a curva C que estamos trabalhando.
  2. Substituir os termos do campo vetorial F → x ,   y ,   z pelos termos da parametrização.
  3. Encontrar o termo d r → .

Então vem comigo nessa aventura! :D

Passo 2

Vamos então parametrizar a curva C , mas por falar nisso, quem é a curva C ?

Como nos pediu o exercício, a curva é dado pela interseção do paraboloide de equação z = x 2 + y 2

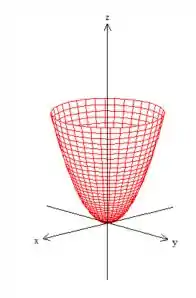
com esse plano 4 x + 2 y + z = 1 , bonitinho aqui:

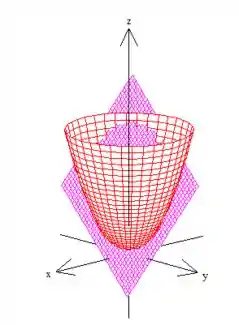
Sacou? :D

Passo 3

Como já comentamos no passo anterior, necessitamos da parametrização da curva. Bem, estamos falando de uma curva que é a interseção de duas superfícies, e em matemática, essa intercessão se dá pelo sistema:

z = x 2 + y 2 4 x + 2 y + z = 1         →

Isolando z na de baixo...

4 x + 2 y + z = 1         →               z = 1 - 4 x - 2 y

substituindo na primeira...

z = x 2 + y 2         →           1 - 4 x - 2 y = x 2 + y 2

Onde esta equação aí, nos representa uma elipse no plano x y , quer ver?

    1 - 4 x - 2 y = x 2 + y 2       →             1 = x 2 + 4 x + y 2 + 2 y

Completando quadrado lembrando que x 2 + 4 x = x + 2 2 - 4 e y 2 + 2 y = y + 1 2 - 1 ...

    1 = x 2 + 4 x + y 2 + 2 y       →               1 = x + 2 2 - 4 + y + 1 2 - 1     →

x + 2 2 + y + 1 2 = 6

Viu! Uma elipse, ou melhor, uma circunferência (circunferências são elipses também ) de raio 6 , mas centrada no ponto - 2 ,   - 1 :

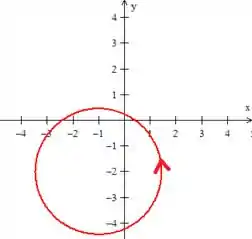
Veja que essa circunferência é a projeção da curva no espaço...

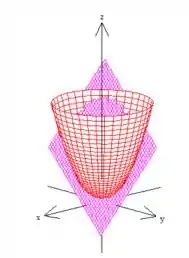
no plano X Y (não se preocupe tanto com o desenho, isso é só um esboço ), e por isso ela gira no sentido horário, sacou?

Se estivéssemos trabalhando com a circunferência no centro, sua parametrização seria:

x = R a i o   d a   c i r c u n f e r ê n c i a ⋅ cos ⁡ t = 6 cos ⁡ t

y = R a i o   d a   c i r c u n f e r ê n c i a ⋅ sin ⁡ t = 6 sin ⁡ t

Mas estamos deslocados de um ponto - 2 ,   - 1 , logo...

x = 6 cos ⁡ t - 2

y = 6 sin ⁡ t - 1

Quanto ao z ...

  z = 1 - 4 x - 2 y       →         z = 1 - 4 6 cos ⁡ t - 2 - 2 6 sin ⁡ t - 1

z = 11 - 4 6 cos ⁡ t - 2 6 sin ⁡ t

Logo a parametrização bonitinha é...

γ t = 6 cos ⁡ t - 2   ,   6 sin ⁡ t - 1   ,   11 - 4 6 cos ⁡ t - 2 6 sin ⁡ t  

Como a circunferência é completa, t , dá uma volta completa...

0 ≤ t ≤ 2 π

Passo 4

Beleza! Agora devemos prosseguir substituindo no campo vetorial F → x ,   y ,   z , esse x , y e z pelos termos da parametrização:

F → x ,   y ,   z = z ,   x ,   y   →

Lembrando que 6 cos ⁡ t - 2   ,   6 sin ⁡ t - 1   ,   11 - 4 6 cos ⁡ t - 2 6 sin ⁡ t   = x ,   y ,   z ...

F → γ t = 11 - 4 6 cos ⁡ t - 2 6 sin ⁡ t , 6 cos ⁡ t - 2   , 6 sin ⁡ t - 1

Passo 5

Para encontrar o termo d r → , basta sabermos que facilmente o encontramos fazendo:

d r → = γ ' t d t

Como no caso a parametrização foi

γ t = 6 cos ⁡ t - 2   ,   6 sin ⁡ t - 1   ,   11 - 4 6 cos ⁡ t - 2 6 sin ⁡ t  

Derivando cada termo do vetor em relação à t ...

  γ ' t = - 6 sin ⁡ t , 6  cos ⁡ t ,   4 6  sin ⁡ t - 2 6 cos ⁡ t

Agora, detalhe importante: como a circunferência gira no sentido horário, temos que trocar o sinal desse vetor multiplicando por - 1 cada entrada, ok?

γ ' t = 6 sin ⁡ t , - 6  cos ⁡ t ,   - 4 6  sin ⁡ t + 2 6 cos ⁡ t

d r → = 6 sin ⁡ t , - 6  cos ⁡ t ,     2 6 cos ⁡ t - 4 6  sin ⁡ t d t

Passo 6

Voltando para a integral de linha que estamos trabalhando

∫ C   F → x ,   y ,   z d r →

e substituir todos os dados que obtivemos...

∫ 0 2 π 11 - 4 6 cos ⁡ t - 2 6 sin ⁡ t , 6 cos ⁡ t - 2   , 6 sin ⁡ t - 1 ∙ 6 sin ⁡ t , - 6  cos ⁡ t ,     2 6 cos ⁡ t - 4 6  sin ⁡ t d t

Não se esqueça de realizar esse produto escalar de vetores aí, heim!

∫ 0 2 π 11 - 4 6 cos ⁡ t - 2 6 sin ⁡ t 6 sin ⁡ t + 6 cos ⁡ t - 2 - 6  cos ⁡ t + 6 sin ⁡ t - 1   2 6 cos ⁡ t - 4 6  sin ⁡ t d t =

Não desanima porque essas coisas vão melhorar:

∫ 0 2 π 11 6 sin ⁡ t - 24 cos ⁡ t sin ⁡ t - 12 sin 2 ⁡ t + - 6 cos 2 ⁡ t + 2 6  cos ⁡ t +   12 cos ⁡ t sin ⁡ t - 24   sin 2 ⁡ t - 2 6 cos ⁡ t + 4 6 sin ⁡ t d t =

∫ 0 2 π 15 6 sin ⁡ t - 12 cos ⁡ t sin ⁡ t - 36 sin 2 ⁡ t - 6 cos 2 ⁡ t d t =

separando esse - 36 sin 2 ⁡ t = - 30 sin 2 ⁡ t - 6 sin 2 ⁡ t ...

∫ 0 2 π 15 6 sin ⁡ t - 12 cos ⁡ t sin ⁡ t - 3 0 sin 2 ⁡ t - 6 sin 2 ⁡ t - 6 cos 2 ⁡ t d t =

∫ 0 2 π 15 6 sin ⁡ t - 12 cos ⁡ t sin ⁡ t - 30 sin 2 ⁡ t - 6 sin 2 ⁡ t + cos 2 ⁡ t d t =

∫ 0 2 π 15 6 sin ⁡ t - 12 cos ⁡ t sin ⁡ t - 30 sin 2 ⁡ t - 6 d t

Não disse que ia simplificar? Agora é só resolver essa integral aí e correr par o abraço!

∫ 0 2 π 15 6 sin ⁡ t - 6 d t - 12 ∫ 0 2 π cos ⁡ t sin ⁡ t d t - 30 ∫ 0 2 π sin 2 ⁡ t d t

Passo 7

Vamos aqui calcular essa primeira integral aqui ∫ 0 2 π 15 6 sin ⁡ t - 6 d t !

Bem, ela é direta, então:

∫ 0 2 π 15 6 sin ⁡ t - 6 d t = - 15 6 cos ⁡ t - 6 t 0 2 π =

- 15 6 cos ⁡ 2 π - 6 2 π - - 15 6 cos ⁡ 0 - 6 0 =

- 12 π

Passo 8

Agora vamos brincar com a segunda ∫ 0 2 π cos ⁡ t sin ⁡ t d t !

Repare que podemos fazer aí uma mudança simples:

sin ⁡ t = u         →               d u = cos ⁡ t d t

Não se esqueça de mudar os limites também, heim!

t = 0         →           sin ⁡ 0 = 0 = u

t = 2 π         →           sin ⁡ 2 π = 0 = u

Repare que o limite de u ficou o mesmo, e como a função é continua (produto de seno por cosseno), podemos afirmar que:

∫ 0 2 π cos ⁡ t sin ⁡ t d t = 0

Passo 9

Passando agora pela última!

∫ 0 2 π sin 2 ⁡ t d t

Lembrando que sin 2 ⁡ t = 1 - cos ⁡ ( 2 t ) 2 ...

∫ 0 2 π 1 - cos ⁡ 2 t 2 d t = 1 2 t - sin ⁡ 2 t 2 ⋅ 1 2 0 2 π =

1 2 2 π - sin ⁡ 4 π 2 ⋅ 1 2 - 1 2 0 - sin ⁡ 0 2 ⋅ 1 2 =

esses senos todos zeram, sobrando...

π

Passo 10

Juntando tudo:

∫ C   F → x ,   y ,   z d r → = ∫ 0 2 π 15 6 sin ⁡ t - 6 d t - 12 ∫ 0 2 π cos ⁡ t sin ⁡ t d t - 30 ∫ 0 2 π sin 2 ⁡ t d t =

- 12 π - 12 0 - 30 π =

- 42 π

Resposta

c )     - 42 π

Exercícios de Livros Relacionados

A base de uma cerca circular de raio 10 m é dada por x = 10 c o s t ,y = 10 s e n t . A altura da cerca na posição x , y é dada pela função h x , y = 4 + 0,01 ( x 2 - y 2 ) , portanto a altura varia 3
Use uma calculadora para avaliar a integral de linha correta até quatro casas decimais. ∫ C x y arctan ⁡ z d s, onde C tem equações paramétricas x = t 2, y = t 3, z = t, 0 ≤ t ≤ π 4
Calcule o valor da integral de linha, onde C é a curva dada. ∫ C x y e y z d y C :x = t , y = t 2 , z = t 3 , 0 ≤ t ≤ 1
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 + z 2 )d s , onde C é a interseção das superfícies x 2 16 + y 2 9 + z 2 16 = 1ey = 2 .
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 - z )d s , onde C é a parte da interseção das superfícies x 2 + y 2 + z 2 = 8 zez = 4