Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial no R²

Ver Teoria
Exercício 171234567891011121314151618192021222324252627282930313233343536373839404142434445

Enunciado

  1. Calcule ∮ C   - y   d x + x   d y , ao longo dos seguintes caminhos fechados, orientados no sentido anti-horário.
  1. circunferência de centro na origem e raio 2 .

Passo 1

Bem, antes do começarmos qualquer coisa, vamos colocar essa integral de linha de uma forma mais elegante.

Como você já pode notar, a integral de linha está assim ∮ C   - y   d x + x   d y , certo? Só que esse formato é apenas outra forma de falar que estamos trabalhando uma integral de linha de um campo de vetores: ∮ C   F → x ,   y d r →

∮ C   - y   d x + x   d y = ∮ C   F → x ,   y d r →

Onde esse F → x ,   y é o vetor...

F → x ,   y = - y ,   x

Se buscamos a solução dessa integral de linha do modo diretão, nada mais justo que seguirmos o passo a passo maroto de resolução desse tipo de integral:

  1. Parametrizar a curva C que estamos trabalhando
  2. Substituir os termos do campo vetorial F → x ,   y pelos termos da parametrização
  3. Encontrar o termo d r →

Então vem comigo nessa aventura! :D

Passo 2

Vamos então parametrizar a curva C , mas por falar nisso, quem é a curva C ?

Como nos pediu o exercício, a curva é uma circunferência de raio 2 e de centro na origem (não se esqueça de que está está orientada no sentido anti-horário ):

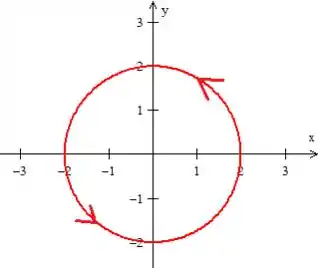
Essa curva pode ser parametrizada semelhantemente as coordenadas polares:

x = R a i o   d a   c i r c u n f e r ê n c i a ⋅ cos ⁡ t

y = R a i o   d a   c i r c u n f e r ê n c i a ⋅ sin ⁡ t

Como ao raio é igual a 2 ...

x = 2 cos ⁡ t

y = 2 sin ⁡ t

então, uma boa parametrização é

γ t = 2 cos ⁡ t ,   2 sin ⁡ t

Lembre-se de que o t sempre sai do eixo x girando no sentido anti-horário, sendo assim, o nosso t tem que dar uma volta completa:

0 ≤ t ≤ 2 π

Passo 3

Beleza! Agora devemos prosseguir substituindo no campo vetorial F → x ,   y , esse x e y pelos termos da parametrização:

F → x ,   y = - y ,   x       →

Como na parametrização que temos,   γ t = 2 cos ⁡ t ,   2 sin ⁡ t , x é a primeira entrada e y é a segunda...

x = 2 cos ⁡ t

y = 2 sin ⁡ t

Basta substituir no campo vetorial:

F → γ t = - 2 sin ⁡ t ,   2 cos ⁡ t

Passo 4

Para encontrar o termo d r → , basta sabermos que facilmente o encontramos fazendo:

d r → = γ ' t d t

No caso a parametrização foi γ t = 2 cos ⁡ t ,   2 sin ⁡ t , derivando cada termo do vetor em relação a t ...

γ t = 2 cos ⁡ t ,   2 sin ⁡ t             →               γ t = - 2 sin ⁡ t , 2 cos ⁡ t

Logo...

d r → = - 2 sin ⁡ t , 2 cos ⁡ t d t

Passo 5

Voltando para a integral de linha que estamos trabalhando

∮ C   F → x ,   y d r →

e substituir todos os dados que obtivemos...

∮ C   F → x ,   y d r → = ∫ 0 2 π - 2 sin ⁡ t ,   2 cos ⁡ t ∙ - 2 sin ⁡ t , 2 cos ⁡ t d t

Não se esqueça de realizar esse produto escalar de vetores aí, heim!

∫ 0 2 π 4 sin 2 ⁡ t +   4 cos 2 ⁡ t d t =

Colocando em evidência o 4 e lembrando que sin 2 ⁡ t + cos 2 ⁡ t = 1 ...

∫ 0 2 π 4 sin 2 ⁡ t +   cos 2 ⁡ t d t = ∫ 0 2 π 4 d t =

4 2 π =

8 π

Resposta

a )   8 π

Exercícios de Livros Relacionados

Determine o trabalho realizado pelo campo de força F x ,y = xs e nyi + yj em uma partícula que se move sobre a parábola y = x 2 de - 1 ,1 a 2 ,4 .
Seja F x , y = - yi + xj x 2 + y 2 Mostre que ∂ P / ∂ y = ∂ Q / ∂ x .Mostre que ∫ C F ⋅ d r não é independente do caminho. [Sugestão: calcule ∫ C 1 F ⋅ d r e ∫ C 2 F ⋅ d r onde C 1 e C 2 são as metade
Mostre que um campo de força constante realiza trabalho nulo sobre uma partícula que dá uma única volta completa uniformemente na circunferência x 2 + y 2 = 1 .Isso também é verdadeiro para um campo d
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = 3 + 2 x y 2 i → + 2 x 2 y j → , C é o arco da hipérbole y = 1 x de ( 1,1 ) a
Mostre que a integral de linha é independente e calcule a integral. ∫ C 2 x s e nyd x + ( x 2 cos ⁡ y - 3 y 2 ) d y C é qualquer caminho de ( - 1,0 ) a ( 5,1 )