Se é a região interior a elipse e exterior à circunferência , calcule a integral de linha
Onde está positivamente orientada.
Passo 1
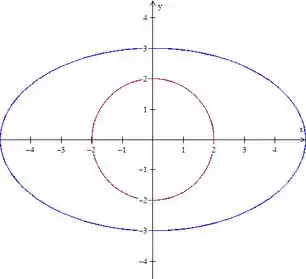
Vamos antes de mais nada fazer um esboço da região e da elipse, , e da circunferência, .
Passo 2
Como temos uma integral de linha, podemos tentar empregar a técnica normal e sair parametrizando as curvas.
Como eu não consigo parametrizar a elipse e a circunferência ao mesmo tempo, vou precisar separar a integral em duas (uma para cada curva). Isso vai dar um trabalhão de conta! Então, para facilitar, vou usar o teorema de Green.
Passo 3
Antes de sair usando o teorema de Green, precisamos garantir que a curva está fechada (como é uma elipse e uma circunferência tá tudo certo) e positivamente orientada (o enunciado já garante isso pra gente :D). Além disso, o campo tem que estar bem definido em . Como não tem divisão por zero, raiz negativa nem nada do tipo tá tudo certo e podemos mandar bala no teorema que diz:
Passo 4
Agora a nossa missão é calcular a integral dupla na esquerda! Para isso, primeiro vamos calcular o integrando alí
Então, vamos ter o seguinte
Onde é a área de
Passo 5
Beleza, mas como calculo essa área? Cara a gente pode lembrar lá da geometria e fazer a área da elipse menos a área do círculo. Para quem não lembra a área de uma elipse vai ser
No nosso caso, temos que e . Vamos ficar então com
Logo,