29) Calcule
onde é o arco da parábola de a .
Passo 1
Bem, perceba que nesse problema o enunciado não nos disse como essa integral de linha deve ser feita, porém... Repare que o campo que estamos trabalhando é estranho:
Isso é uma sugestão que devemos utilizar o teorema de Green para matar o problema, mas para você ter certeza se é Green ou não, calculemos
As derivadas parciais são...
logo
De fato é muito simples essa subtração nos indicando que de fato estamos lidando com Green
Passo 2
O teorema de Green nada mais é do que essa igualdade mara entre a integral de linha com uma integral dupla:
Mas antes de aplicarmos essa igualdade maravilhosa do Teorema, temos que avalizar as condições de Green, que sempre nos exige:
1º - Uma região fechada que tem com borda, a curva fechada .
2º - Orientadas positivamente.
3º - Um campo sem singularidades onde estamos trabalhando.
Vamos averiguar?
Passo 3
O primeiro, como vimos, nos diz que precisamos de uma curva fechada e delimitando uma região .
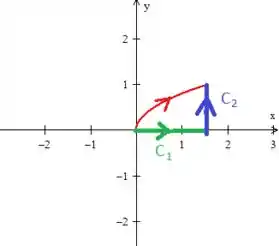
Ora, a curva , pelo próprio enunciado, é um pedacinho de parábola invertida ao redor de indo do ponto ao :
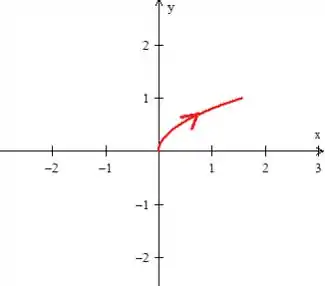
Observe que infelizmente essa curva é aberta e não poderíamos aplicar o teorema. Por isso, nos devemos fecha-la com a curva mais simples que conseguirmos o que no caso são essas duas retinhas aqui:
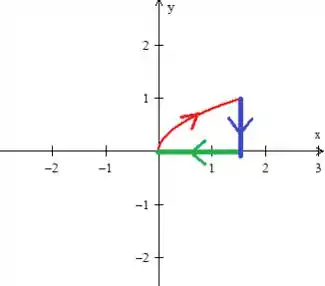
Repare que ela tem que está seguindo o fluxo e, além disso, ela delimita essa região fechada :
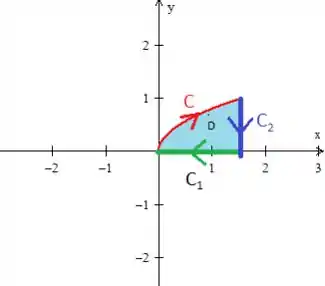
Passo 4
Quanto ao orientada positivamente, infelizmente não está ok. Afinal de contas à borda gira no sentido horário, mas... Para concertar esse fato é bem easy, basta trocar o sinal da integral dupla...
O campo ...
Também não tem problema algum, podendo então prosseguir com a igualdade!
Passo 5
Condições do Teorema sendo satisfeitas, podemos aplicar a igualdade numa boa:
Bem, cuidado que aqui tem um detalhe muito importante! Se você reparar a região com mais cuidado,
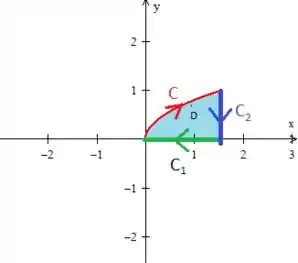
verá que a fronteira dele é a curva em vermelho e as retas as quais nomearemos de e ...
Outro detalhe que ajuda é trocar aqueles sinais de menos na integral de linha invertendo o sentido de giro das curvas e ...
Representadas na matemática com um sinal de menos...
Se queremos a integral de linha em , calculemos essas integrais do lado direito e tá tudo certo. Bora?
Passo 6
Primeiro, a mais fácil, a integral dupla:
Digo fácil, pois substituindo...
Sacou?
Passo 7
Agora a integral de linha em ...
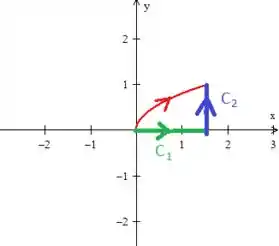
- Precisamos de parametrizada:
- O termo é...
- Não se esqueça de trocar os termos da função ...
- Precisamos de parametrizada:
- O termo é...
- Não se esqueça de trocar os termos da função ...
ou
como estamos sando de e indo para varia de a , logo...
Substituindo na integral de linha...
Passo 8
Repetir o processo para ...
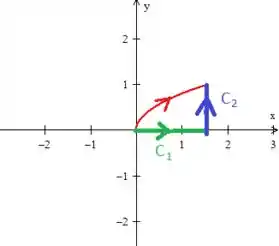
ou
como estamos sando de e indo para varia de a , logo...
Substituindo na integral de linha...
Passo 8
Voltando ao teorema de Green...
e substituindo esses resultados paralelos...