Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial no R²

Ver Teoria
Exercício 101234567891112131415161718192021222324252627282930313233343536373839404142434445

Enunciado

  1. Achar o trabalho de uma força variável, dirigida para a origem das coordenadas, cuja grandeza é proporcional ao afastamento do ponto em relação à origem das coordenas, se o ponto de aplicação desta força descreve, no sentido anti-horário, a parte da elipse x 2 4 + y 2 16 = 1 no primeiro quadrante.

Passo 1

Para acharmos o trabalho de F → devemos fazer a integral de linha de F → ao longo da curva C que é a curva onde queremos que seja calculado o trabalho, no caso, aquele pedacinho de elipse:

T r a b a l h o = ∫ C   F → d r →

Encontrar uma solução para uma integral de linha nada mais é do que seguir um passo a passo maroto:

  1. Parametrizar a curva C que estamos trabalhando.
  2. Substituir os termos do campo vetorial F → x ,   y pelos termos da parametrização.
  3. Encontrar o termo d r → .

Mas aqui teremos um trabalho extra, que é justamente desvendar quem é o campo vetorial de forças F → ! Então vem comigo nessa aventura! :D

Passo 2

Bem, antes de passarmos para a matemática da coisa (resolver o passo a passo da integral de linha), vamos determinar quem é o campo vetorial F → de forças. Pra isso, basta seguir as instruções do enunciado:

Mas antes, vamos falar que o campo de força tem essa cara aqui: F → = a   i → + b j → ( a e b aqui é algo genérico, tá? a gente já vai ver quem eles são).

O problema nos fala que essa força está apontando para a origem:

Isso quer dizer que devemos inverter os sinais do nosso campo: F → = - a   i → - b j → , saca?

Outra informação, foi que a grandeza (a força, no caso) é proporcional ao afastamento do ponto em relação a origem, e cara, o que dá esse afastamente é justamente a coordenada do ponto: ( x ,   y ) !

Basta você pensar que o ponto ( 0 ,   1 ) está afastado 1 unidade em y e 0 unidades em x da origem, saca?

Logo:

F → = - k x   i → - k y j →

k é a constante de proporcionalidade!

Passo 3

Podemos então resolver a integral e sabemos para isso que devemos parametrizar a curva que estamos trabalhando.

Como a curva é esse pedacinho de elipse

x 2 4 + y 2 16 = 1   →

x 2 2 2 + y 2 4 2 = 1  

no primeiro quadrante...

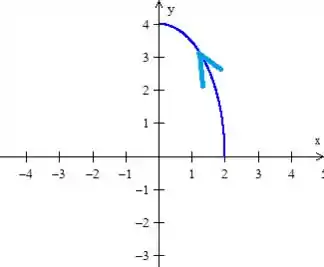
Sua parametrização sai direta com a parametrização de elipses, onde trocamos:

x = 2 cos ⁡ t

y = 4 sin ⁡ t

Ou... Colocando de uma forma mais bonitinha...

γ t = 2 cos ⁡ t , 4 sin ⁡ t

Repare na elipse novamente que t varia de 0 até 90 ° ...

0 ≤ t ≤ π 2

Passo 4

Beleza! Agora devemos prosseguir substituindo no campo vetorial F → x ,   y , esse x e y pelos termos da parametrização:

F → x ,   y = - k x ,   - k y

F → γ t = - 2 k cos ⁡ t ,   - 4 k sin ⁡ t

Passo 5

Para encontrar o termo d r → , basta sabermos que facilmente o encontramos fazendo:

d r → = γ ' t d t

Como no caso a parametrização foi γ t = 2 cos ⁡ t , 4 sin ⁡ t , derivando cada termo do vetor em relação a t ...

γ t = 2 cos ⁡ t , 4 sin ⁡ t             →               γ ' t = - 2 sin ⁡ t , 4 cos ⁡ t  

Logo...

d r → = - 2 sin ⁡ t , 4 cos ⁡ t   d t

Passo 6

Voltando para a integral de linha que estamos trabalhando

∫ C   F → x ,   y d r →

e substituir todos os dados que obtivemos...

∫ C   F → x ,   y d r → = ∫ 0 π 2 - 2 k cos ⁡ t ,   - 4 k sin ⁡ t ∙ - 2 sin ⁡ t , 4 cos ⁡ t   d t

Não se esqueça de realizar esse produto escalar de vetores aí, heim!

∫ 0 π 2 - 2 k cos ⁡ t ,   - 4 k sin ⁡ t ∙ - 2 sin ⁡ t , 4 cos ⁡ t   d t = ∫ 0 π 2 4 k cos ⁡ t sin ⁡ t - 16 k cos ⁡ t sin ⁡ t d t =

- 12 k ∫ 0 π 2 cos ⁡ t sin ⁡ t d t

Agora é só resolver a integral e correr para o abraço! :D

Fazendo uma substituição do tipo:

sin ⁡ t = u             →

d u = cos ⁡ t d t

Não se esqueça dos limites:

t = 0             →               u = sin ⁡ 0 = 0

t = π 2             →               u = sin ⁡ π 2 = 1

- 12 k ∫ 0 π 2 cos ⁡ t sin ⁡ t d t =

- 12 k ∫ 0 1 u d u

- 12 k u 2 2 0 1 =

- 6 k

Resposta

- 6 k

Exercícios de Livros Relacionados

Determine o trabalho realizado pelo campo de força F x ,y = xs e nyi + yj em uma partícula que se move sobre a parábola y = x 2 de - 1 ,1 a 2 ,4 .
Seja F x , y = - yi + xj x 2 + y 2 Mostre que ∂ P / ∂ y = ∂ Q / ∂ x .Mostre que ∫ C F ⋅ d r não é independente do caminho. [Sugestão: calcule ∫ C 1 F ⋅ d r e ∫ C 2 F ⋅ d r onde C 1 e C 2 são as metade
Mostre que um campo de força constante realiza trabalho nulo sobre uma partícula que dá uma única volta completa uniformemente na circunferência x 2 + y 2 = 1 .Isso também é verdadeiro para um campo d
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = 3 + 2 x y 2 i → + 2 x 2 y j → , C é o arco da hipérbole y = 1 x de ( 1,1 ) a
Mostre que a integral de linha é independente e calcule a integral. ∫ C 2 x s e nyd x + ( x 2 cos ⁡ y - 3 y 2 ) d y C é qualquer caminho de ( - 1,0 ) a ( 5,1 )