Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar R³

Ver Teoria
Exercício 171234567891011121314151618192021222324252627282930313233343536373839404142434445464748

Enunciado

  1. Calcule

∫ C   P   d x + Q   d y + R   d z

Onde:

  1. F → = P ,   Q ,   R = - 2 y ,   z ,   x e C é a interseção das superfícies 4 x 2 + y 2 = 1 e y 2 + z 2 = 1 , com x ≥ 0 e z ≥ 0 , percorrida uma vez do ponto 0 ,   - 1 ,   0 ao 0 ,   1 ,   0 .

Passo 1

Bem, antes do começarmos qualquer coisa, vamos colocar essa integral de linha de uma forma mais elegante.

Como você já pode notar, a integral de linha está assim ∫ C   P   d x + Q   d y + R   d z , certo? Só que esse formato é apenas outra forma de falar que estamos trabalhando uma integral de linha de um campo de vetores: ∫ C   F → x ,   y ,   z d r →

∫ C   P   d x + Q   d y + R   d z = ∫ C   F → x ,   y ,   z d r →

Onde esse F → x ,   y ,   z é o vetor...

F → x ,   y ,   z = - 2 y ,   z ,   x

Se buscamos a solução dessa integral de linha do modo diretão, nada mais justo que seguirmos o passo a passo maroto de resolução desse tipo de integral:

  1. Parametrizar a curva C que estamos trabalhando.
  2. Substituir os termos do campo vetorial F → x ,   y ,   z pelos termos da parametrização.
  3. Encontrar o termo d r → .

Então vem comigo nessa aventura! :D

Passo 2

Vamos então parametrizar a curva C , mas por falar nisso, quem é a curva C ?

Como nos pediu o exercício, a curva é esse trechinho encontrado fazendo a intercessão desse cilindro centrado em z : 4 x 2 + y 2 = 1

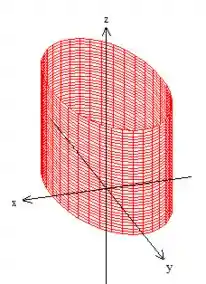
com esse outro cilindro centrado em x : y 2 + z 2 = 1

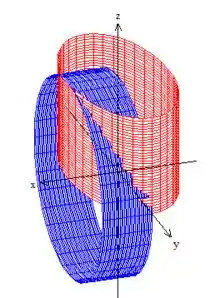
Lembre-se que estamos trabalhando com essa parte onde x ≥ 0 e z ≥ 0 , dando pra gente, essa curva aí, oh:

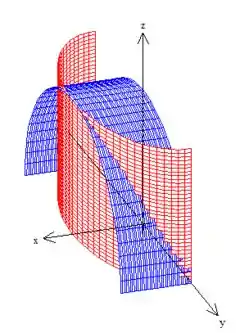
Sacou? :D

Passo 3

Como já comentamos no passo anterior, necessitamos da parametrização da curva. Bem, estamos em cima do cilindro vermelho de equação 4 x 2 + y 2 = 1 . Repare que no plano X Y , essa equação é essa elipse aqui, oh:

E poh, parametrizar elipses sabemos que necessitamos da equação na sua forma geral: x 2 a 2 + y 2 b 2 = 1 , então:

4 x 2 + y 2 = 1     →     x 2 1 4 + y 2 = 1       →

x 2 1 2 2 + y 2 1 2 = 1

Agora sua parametrização sempre será:

x = a cos ⁡ t

y = b sin ⁡ t

como podemos ver a = 1 2 e b = 1 ...

x = 1 2 cos ⁡ t

y = sin ⁡ t

Perceba que ainda falta definirmos quem será o z nessa brincadeira. Logo, venha comigo!

Passo 4

Pow, o z , note no esboço da curva C , que ele está na interseção dos dois cilindros

Resolver uma interseção em Matemática é resolver o sistema com as equações das superfícies envolvidas:

4 x 2 + y 2 = 1 y 2 + z 2 = 1

Isolando y 2 na primeira...

y 2 = 1 - 4 x 2

e substituindo na segunda:

y 2 + z 2 = 1           →               1 - 4 x 2 + z 2 = 1           →

- 4 x 2 + z 2 = 0         →

z 2 = 4 x 2

extraindo a raiz...

z = ± 4 x 2 = ± 2 x

como estamos trabalhando com a parte de cima...

z = 2 x

z = 2 1 2 cos ⁡ t =

cos ⁡ t

Logo, a parametrização final é:

γ t = 1 2 cos ⁡ t , sin ⁡ t ,   cos ⁡ t

Passo 5

Lembre-se que nunca devemos sair de uma parametrização sem antes dizermos onde o parâmetro, que no caso é o t , está variando, heim!

Essa informação, podemos tirar da informação dos pontos que curva varia:

0 ,   - 1 ,   0         ⇒ E   v a i   a t é …             0 ,   1 ,   0

Substituindo o primeiro ponto na curva:

0 ,   - 1 ,   0 = 1 2 cos ⁡ t , sin ⁡ t ,   cos ⁡ t

Vemos que o cosseno tem que ser 0 e o seno - 1 , onde isso acontece? Sim! Em - 90 ° !

Com o ponto de chegada, encontramos o t de chegada:

0 ,   1 ,   0 = 1 2 cos ⁡ t , sin ⁡ t ,   cos ⁡ t

Novamente, cosseno 0 , mas o seno 1 ... t = 90 ° !

Então podemos falar que o t está variando de...

- 90 ° ≤ t ≤ 90 °

ou...

- π 2 ≤ t ≤ π 2

Passo 6

Beleza! Agora devemos prosseguir substituindo no campo vetorial F → x ,   y ,   z , esse x , y e z pelos termos da parametrização:

F → x ,   y ,   z = - 2 y ,   z ,   x   →

Lembrando que 1 2 cos ⁡ t , sin ⁡ t ,   cos ⁡ t = x ,   y ,   z ...

F → γ t = - 2 sin ⁡ t , cos ⁡ t , 1 2 cos ⁡ t

Passo 7

Para encontrar o termo d r → , basta sabermos que facilmente o encontramos fazendo:

d r → = γ ' t d t

Como no caso a parametrização foi γ t = 1 2 cos ⁡ t , sin ⁡ t ,   cos ⁡ t , derivando cada termo do vetor em relação à t ...

γ t = 1 2 cos ⁡ t , sin ⁡ t ,   cos ⁡ t             →               γ ' t = - 1 2 sin ⁡ t , cos ⁡ t ,   - sin ⁡ t

Logo...

d r → = - 1 2 sin ⁡ t , cos ⁡ t ,   - sin ⁡ t d t

Passo 8

Voltando para a integral de linha que estamos trabalhando

∫ C   F → x ,   y ,   z d r →

e substituir todos os dados que obtivemos...

∫ C   F → x ,   y ,   z d r → = ∫ - π 2 π 2 - 2 sin ⁡ t , cos ⁡ t , 1 2 cos ⁡ t ∙ - 1 2 sin ⁡ t , cos ⁡ t ,   - sin ⁡ t d t

Não se esqueça de realizar esse produto escalar de vetores aí, heim!

∫ - π 2 π 2 - 2 sin ⁡ t , cos ⁡ t , 1 2 cos ⁡ t ∙ - 1 2 sin ⁡ t , cos ⁡ t ,   - sin ⁡ t d t

= ∫ - π 2 π 2 sin 2 ⁡ t + cos 2 ⁡ t - 1 2 sin ⁡ t cos ⁡ t   d t =

Como sin 2 ⁡ t + cos 2 ⁡ t = 1 ...

∫ - π 2 π 2 1 - 1 2 sin ⁡ t cos ⁡ t   d t

Agora basta que resolva a integral e corra para o abraço!

∫ - π 2 π 2 1 - 1 2 sin ⁡ t cos ⁡ t   d t = ∫ - π 2 π 2 1   d t + 1 2 ∫ - π 2 π 2 - sin ⁡ t cos ⁡ t   d t   →

∫ - π 2 π 2 1 - 1 2 sin ⁡ t cos ⁡ t   d t = π 2 - - π 2 + 1 2 ∫ - π 2 π 2 - sin ⁡ t cos ⁡ t   d t   →

∫ - π 2 π 2 1 - 1 2 sin ⁡ t cos ⁡ t   d t = π + 1 2 ∫ - π 2 π 2 - sin ⁡ t cos ⁡ t   d t

Quanto a essa segunda integral, vou te dar um bizuzão:

O sin ⁡ t é uma função impar (tem o gráfico simétrico na origem) e o cosseno é par (simétrico no eixo y ). “Impar × par = impar” e a integral simétrica (indo de um numero negativo até o mesmo número positivo como - π 2 até π 2 ) é sempre 0 :

∫ - π 2 π 2 1 - 1 2 sin ⁡ t cos ⁡ t   d t = π + 0 =

∫ - π 2 π 2 1 - 1 2 sin ⁡ t cos ⁡ t   d t = π

Pode conferir fazendo a integral pela substituição: cos ⁡ t = u     →         d u = - sin ⁡ t d t !

Resposta

b )   π

Exercícios de Livros Relacionados

A base de uma cerca circular de raio 10 m é dada por x = 10 c o s t ,y = 10 s e n t . A altura da cerca na posição x , y é dada pela função h x , y = 4 + 0,01 ( x 2 - y 2 ) , portanto a altura varia 3
Use uma calculadora para avaliar a integral de linha correta até quatro casas decimais. ∫ C x y arctan ⁡ z d s, onde C tem equações paramétricas x = t 2, y = t 3, z = t, 0 ≤ t ≤ π 4
Calcule o valor da integral de linha, onde C é a curva dada. ∫ C x y e y z d y C :x = t , y = t 2 , z = t 3 , 0 ≤ t ≤ 1
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 + z 2 )d s , onde C é a interseção das superfícies x 2 16 + y 2 9 + z 2 16 = 1ey = 2 .
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 - z )d s , onde C é a parte da interseção das superfícies x 2 + y 2 + z 2 = 8 zez = 4