Seja uma curva simétrica em relação ao eixo , que vai de a , como mostrada na figura abaixo. Sabendo-se que a área da região delimitada por e o eixo vale 16, calcule o trabalho realizado pela força
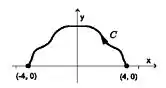
Passo 1
De cara sabemos aqui que vamos precisar usar o teorema de Green, pois veja que as únicas informações que o enunciado nos deu foi que a função é simétrica e que a área é 16. O teorema de Green nos diz que
O primeiro problema é que essa curva deveria ser fechada, que não é o nosso caso. Vamos ter que fecha-la antes de começar a usar o teorema.
A forma mais simples de fechar uma curva é simplesmente ligar os ponto, ou seja, criar uma reta de até , olha o esboço
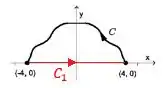
O teorema vai ficar assim, então
Vamos fazer essa integral de linha e essa dupla passo a passo aqui com bastante calma pra você enteder tudo, vamos nessa?
Passo 2
Vamos começar aqui pela integral de linha
Precisamos primeiramente de uma parametrização de , sabemos que ela é uma reta que liga até , podemos parametrizar isso aí assim
O campo com esses parâmetros fica assim
Essa função não é muito comum pra gente, . Quando você se deparar com essas funções, faz como se fosse uma pergunta pra você mesmo. Nesse caso seria: “Qual o arco(ângulo) cuja tangente é zero?”
Sabemos que somento o ângulo 0 tem tal tangente, portanto
Voltando para o nosso campo
Beleza, precisamos ainda da derivada da parametrização da reta
Juntando tudo na integral de linha
Passo 3
Agora é só calcular essa integral
Passo 4
Beleza, vamos agora pra parte mais difícil, essa integral dupla aqui
Vamos começar vendo quanto é esse termo ai de dentro
Então a nossa integral dupla vai ficar
Separando isso aí um pouquinho
Olha que bom! Apareceu a tal área que o enunciado tinha falado pra gente que valia
Beleza, mas ainda tá faltando aquele termo ali que não faço ideia como integrar! Como faz isso?
Aqui é que entra uma sacada que a questão fala e a gente quase sempre ignora: o enunciado disse que a curva é simétrica em relação ao eixo , isso quer dizer que
Colocando o esboço aqui pra você entender melhor
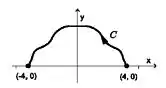
Esse lado direito da função seria , enquanto esse lado esquerdo seria , faz sentido certo? Se a gente definir essa região pelo tipo fica assim
E quais seriam os limites de ? Bom, vamos ver que isso não importa muito, vamos deixar como
Onde é aquele ponto máximo de que não sabemos o valor. A integral fica
Passo 5
Vamos começar a integrar isso aí, então
Por isso que não importa muito qual o valor máximo de , a integral de zero, pra qualquer limite, é igual a zero!
Passo 6
Beleza, então, pra fechar essa integral dupla
Passo 7
Voltando para o teorema de Green que escrevemos la em cima