16) Calcule as seguintes integrais:
d)
onde é a fronteira da região limitada por e .
Passo 1
Bem, perceba que nesse problema o enunciado não nos disse como essa integral de linha deve ser feita, porém... Repare que o campo que estamos trabalhando
é muito complicado. Isso é uma sugestão que devemos utilizar o teorema de Green para matar o problema. Mas, para você ter certeza se é Green ou não, calculemos
As derivadas parciais são...
logo
De fato é muito simples essa subtração nos indicando que de fato estamos lidando com Green
Passo 2
O teorema de Green nada mais é do que essa igualdade mara entre a integral de linha com uma integral dupla:
Mas antes de aplicarmos essa igualdade maravilhosa do Teorema, temos que avalizar as condições de Green, que sempre nos exige:
1º - Uma curva fechada delimitando a região .
2º - A curva , orientada positivamente.
3º - Um campo sem singularidades onde estamos trabalhando.
Vamos averiguar?
Passo 3
1º - Precisamos de uma curva fechada e delimitando uma região .
Ora, a curva , pelo próprio enunciado, é a curva composta por essas duas curvas e . A primeira é parecido com uma parábola ao redor de passando por e a segunda é uma reta:
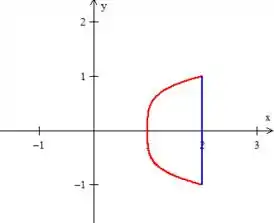
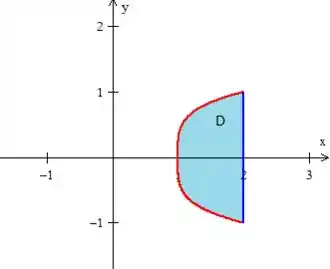
Onde a região é justamente esse espaço:
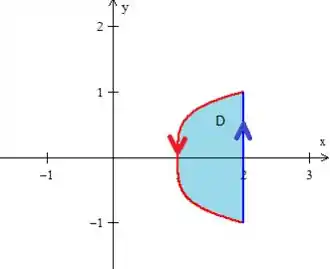
2º - E mais, ela está orientada positivamente sim!!!
Quando o problema não nos fala nada sobre a orientação, assumimos que é no sentido anti-horário, portanto positivamente
3º - O campo que estamos trabalhando...
até tem uma singularidade em ... Como estamos bem longe dele, não tem problema algum.
Passo 4
Condições do Teorema sendo satisfeitas, podemos aplicar a igualdade numa boa:
Se queremos a integral de linha, calculemos a integral dupla e beijinho no ombro ;)
Substituindo...
Para calcular essa integral dupla, devemos descrever a região
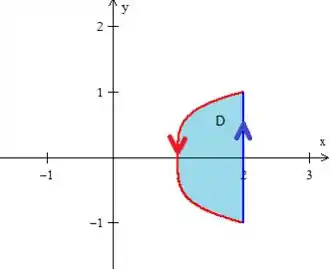
O que pode ser feito utilizando o auxílio de uma região do Tipo ...
O varia do ponto de baixo até o ponto de cima de encontro da parábola com a reta :
então:
Enquanto que o varia da parábola até o ...
Passo 5
Calculando as integrais...