17) Calcule as seguintes integrais:
c)
Onde é a poligonal aberta que une os pontos , e , nesta ordem.
Passo 1
Bem, perceba que nesse problema o enunciado não nos disse como essa integral de linha deve ser feita, porém... Repare que o campo que estamos trabalhando é
e ele é chato!
Isso é uma sugestão que devemos utilizar o teorema de Green para matar o problema, mas para você ter certeza se é Green ou não, calculemos
As derivadas parciais são...
logo
De fato é muito simples essa subtração nos indicando que de fato estamos lidando com Green
Passo 2
O teorema de Green nada mais é do que essa igualdade mara entre a integral de linha com uma integral dupla:
Mas antes de aplicarmos essa igualdade maravilhosa do Teorema, temos que avalizar as condições de Green, que sempre nos exige:
1º - Uma região fechada que tem com borda, a curva fechada .
2º - Orientadas positivamente.
3º - Um campo sem singularidades onde estamos trabalhando.
Vamos averiguar?
Passo 3
O primeiro, como vimos, nos diz que precisamos de uma curva fechada e delimitando uma região .
Ora, a curva , pelo próprio enunciado, é a poligonal aberta que une esses pontos...
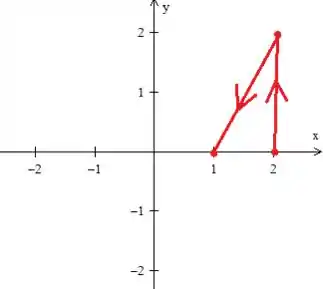
nesse sentido!
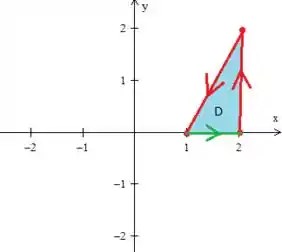
Observe que infelizmente essa curva é aberta e não poderíamos aplicar o teorema. Por isso, nos devemos fecha-la com a curva mais simples que conseguirmos o que no caso é essa retinha verde aqui:
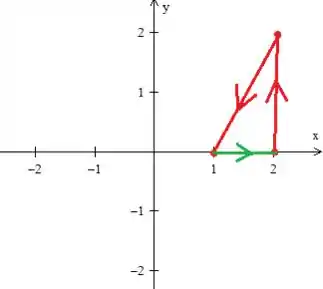
Repare que ela tem que está seguindo o fluxo e, além disso, ela delimita essa região fechada triangular :
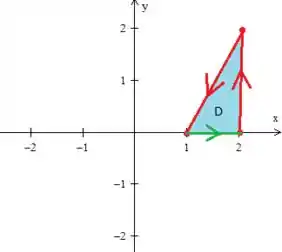
Passo 4
Quanto ao orientada positivamente, está ok, pois a curva gira no sentido anti-horário e em relação ao campo sem singularidades também ok, afinal o nosso campo é:
e ele não tem nenhum “bug” onde estamos trabalhando que é onde os pontos estão positivos ;D
Passo 5
Condições do Teorema sendo satisfeitas, podemos aplicar a igualdade numa boa:
Bem, cuidado que aqui tem um detalhe muito importante! Se você reparar a região com mais cuidado,
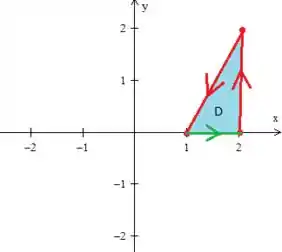
verá que a fronteira dele é a curva em vermelho e a curva verde que vamos chamar de , logo...
Se queremos a integral de linha em , calculemos essas integrais do lado direito e tá tudo certo (hehe ). Bora?
Passo 6
Primeiro, vamos resolver a integral dupla:
Epa! Integral dupla de é a área ! Como a região é camarada...
sua área é:
Onde é a base do triângulo e é . Enquanto ao , sua altura... :
Passo 7
Fazendo agora a integral de linha
em cima da reta que adicionemos...
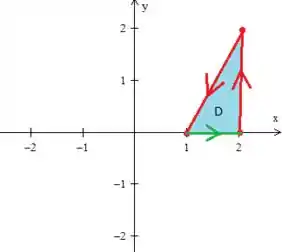
- Precisamos de parametrizada:
- O termo é...
- Não se esqueça de trocar os termos da função ...
ou
como estamos sando de e indo para varia de a , logo...
Substituindo na integral de linha...
Podemos calcular essa integral ai fazendo uma integração por partes...
Voltando para a definida...
Passo 8
Voltando ao teorema de Green...
e substituindo esses resultados paralelos...