Determine o domínio e resolva a seguinte inequação em :
Passo 1
Vamos começar determinando o domínio. Como tempos aqui uma razão de polinômios, o domínio será todo exceto os pontos onde o denominador se anula. Neste caso em:
vamos usar Bhaskara. Temos que
É uma equação na forma:
Com:
Assim, teremos:
Substituindo os valores:
Para cada sinal:
Logo, podemos escrever:
Assim:
Passo 2
Agora, vamos resolver a inequação. Para isso, vamos fatorar o máximo possível. Temos que:
Quanto ao denominador, vamos usar Bhaskara novamente. Temos que:
É uma equação na forma:
Com:
Assim, teremos:
Substituindo os valores:
Opa! Apareceu um número negativo na raiz. Como proceder? Bem, essa raiz de número negativo significa que:
Não possui raiz real, ou seja, seu sinal não muda nunca: ele será sempre positivo ou sempre negativo. Como saber qual o sinal? Só substituir qualquer valor. Vamos escolher , por exemplo:
Assim, vai ser sempre positiva e vamos poder desconsiderar o numerador na nossa tabela.
Passo 3
Temos que nossa inequação equivalente será:
Com raízes:
Então criamos cada um dos intervalos:
Assim, colocamos o intervalo na primeira linha da tabela e os termos na primeira coluna:

Passo 4
Montada a tabela, testamos os sinais de cada termo para cada intervalo. Para o primeiro, queremos . satisfaz, então substituímos:
Assim, teremos:

Para agora, temos que satisfaz. Então:
Assim:

Quase lá, falta . Para esse intervalo, temos que satisfaz. Então:
Assim:

Passo 5
Com os sinais determinados, vamos criar uma nova linha com o sinal equivalente que será o sinal da nossa inequação. Para determinar o sinal equivalente, usamos a regrinha dos sinais:
Assim, vamos ter:
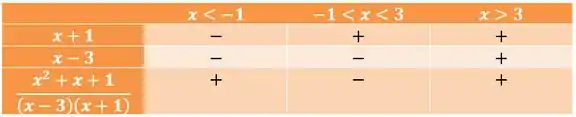
Passo 6
Então, para nossa inequação equivalente:
queremos , então nos interessam os intervalos em que temos o sinal de . Isso corresponde ao intervalo . Além disso, queremos menor ou igual, então nosso ajuste natural seria:
Mas lembra lá do nosso domínio:
e não fazem parte do domínio porque zeram o denominador e provocam uma divisão por zero! Então, apesar de termos , consideramos o intervalo aberto!
Ou então: