Resolva a inequação a seguir e apresente o quadro de sinais e os possíveis valores de x.
Passo 1
Vamos lá!! Temos nessa questão uma inequação envolvendo um produto entre termos:
Onde
Vamos encontrar as raízes de cada uma dessas funções e montar a tabelinha marota para estudar os sinais?!

Passo 2
Vamos encontrar as raízes de cada uma das funções!
Para encontrarmos as raízes da equação
Utilizaremos a fórmula de Bhaskara
Beleza?!

Primeira coisa que precisamos fazer é identificar quem é o , e . Lembra da carinha da nossa equação do 2º grau? Ela tem essa carinha aqui
Então, comparando com a nossa equação
Conseguimos encontrar os valores de , e :
Beleza?! Agora vamos utilizar esses valores para encontrar o :
Substituindo os valores , e , temos
Fazendo as continhas, temos
Agora podemos substituir o valor de e os demais valores na fórmula de Bhaskara:
Teremos então duas raízes:
E
Portanto, as raízes da equação são e !
Visualmente, teríamos
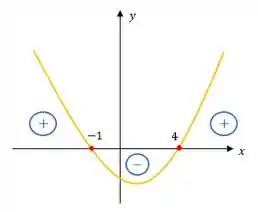
Beleeeza?!
Passo 3
Agora precisamos encontrar a raíz da função
Para isso, iremos igualar a função a
E passar o para o outro lado
O esboço seria
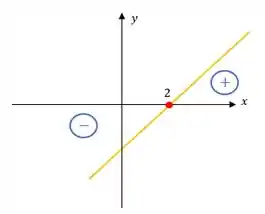
Passo 4
A partir desses valores, vamos montar a tabelinha para estudar os sinais:
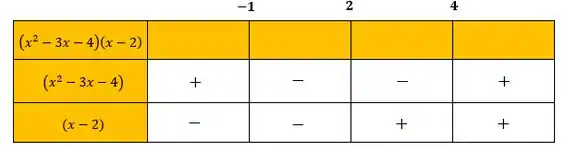
Agora fazendo o estudo dos sinais, teremos
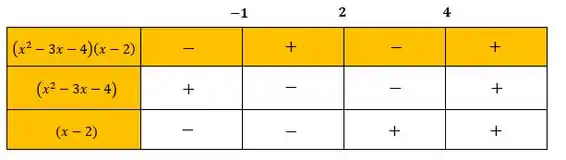
Como queremos
Vamos selecionar os intervalos aonde o sinal é positivo! Assim, nosso conjunto solução é