UTFPR - Cálculo 1 - Provas - P1 - 2019.1 - questão 1b
Estude o sinal das expressões abaixo:
Passo 1
E aii, galerinha!! Como estão? Vamos juntos pra mais uma!!
Pessoal a questão quer que falemos sobre como se comporta o sinal da nossa expressão algébrica em relação aos possíveis valores de . Humm, por onde vocês acham que começamos primeiro?
Passo 2
Gente, minha dica é desmembrar a expressão e analisar de início cada parte separadamente e por fim, iremos visualizar como cada uma dessas partes contribui para o todo dentro da expressão. A nossa expressão é a seguinte :
Vamos analisar primeiro o numerador da expressão: , temos aqui uma função linear do tipo certo?? Vamos montar então o esboço da nossa função linear:
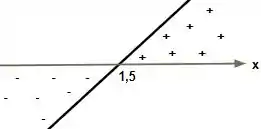
Isso significa que para todo , a imagem da função linear será positiva. E além disso, para todo a imagem da função será negativa.
Passo 3
Agora vamos fazer a mesma coisa para o denominador da fração:. Note que no denominador agora temos um produto de funções lineares do tipo , iremos então encontrar primeiro a função do grau gerada pelo produto dessas funções lineares iniciais.
Agora que encontramos a nossa função do grau do tipo , vamos fazer o esboço do gráfico. Lembrando que o gráfico de uma função do grau é uma parábola.
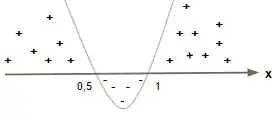
Logo, temos que a imagem só será negativa no intervalo .
Passo 4
Agora vamos juntar em um esboço só as conclusões dos passos anteriores.
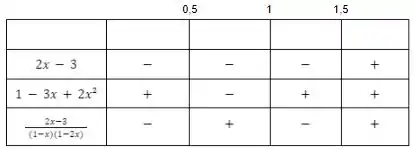
Fazendo o jogo de sinal entre o numerador e o denominador para cada intervalo, descobrimos que a imagem da expressão só será positiva apenas quando .
E aí, tranquilinho?? Bora fazer mais umas então!
Bons Estudos!
Resposta
A imagem da expressão só será positiva apenas quando .