UFPA, Sem Campus, Cálculo I, Listas de Cálculo 1 - Profº Luiz Gutemberg - Lista 01, Questão 1d
Resolva as inequações:
d)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente resolver a inequação que ele nos deu. Repare que temos um quociente de equações formando essa desigualdade.
E quando temos um produto ou um quociente na inequação precisamos fazer a análise de sinal de termo para satisfazer a condição da desigualdade.
Além disso, quando temos um quociente, precisamos tirar o valor de faz o denominador ser zero. Depois montamos o quadro de sinais, colocando na primeira linha e na primeira coluna a função que nós vamos analisar e nas linhas seguintes, as expressões que compõem essa função.
Vamos lá!
Passo 2
Nossa inequação é dada por:
O primeiro termo é e o segunto termo é . Para o primeiro, sua raiz será:
E no segunto termo, teremos a raiz:
Como o é positivo em ambas as funções, ela será crescente e terá valores negativos antes da raiz e terá valores positivos depois. Então, juntando isso no quadro de sinais, temos:
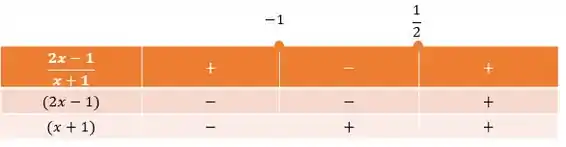
Recapitulando: que nós fizemos foi colocar a função junto com as expressões que a compõe na primeira coluna. Verificamos que por ser positivo em amabas as expressões, o sinal será negativo antes das raízes e positivo depois. E por fim, fizemos o jogo de sinais na primeira linha (sinais diferentes , sinais iguais ).
Só falta um detalhe importante. Como esse é um quociente, o denominador não pode zerar. Isso significa que ele não vai poder assumir o valor da raiz ().
Como nossa condição é de que a função seja menor que zero, ou seja, negativa (), nossa solução será a parte da tabela onde temos o sinal negativo na primeira linha. Assim, temos:
Prontinho, galera! Até a próxima! 😉