Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inequações produto-quociente

Ver Teoria
Exercício 14123456789101112131516171819202122232425262728293031323334353637383940414243444546

Enunciado

UFF, Cálculo IA-Lista 1, GMA, 2008-1, 26

Estude a variação do sinal da função.

f x = ( 2 x - 3 ) ( x + 1 ) ( x - 2 )

Passo 1

Pra resolver essa questão faremos o seguinte: primeiro analisar o sinal de cada termo entre parênteses e depois juntar tudo em um quadrinho para facilitar o estudo do sinal da função f . Vamos começar na ordem que a função foi dada.

2 x - 3 = 0 → x = 3 2

2 x - 3 < 0 → x < 3 2

2 x - 3 > 0 → x > 3 2

Passo 2

x + 1 = 0 → x = - 1

x + 1 < 0 → x < - 1

x + 1 > 0 → x > - 1

Passo 3

x - 2 = 0 → x = 2

x - 2 < 0 → x < 2

x - 2 > 0 → x > 2

Passo 4

Agora vamos juntar tudo no quadro de sinais.

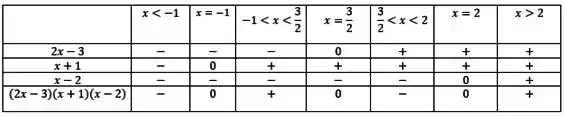A partir desse quadro podemos dizer que:

f ( x ) < 0                     s e   x < - 1   o u   3 2 < x < 2 = 0   s e   x = - 1   o u   x = 3 2   o u   x = 2 > 0                   s e   - 1 < x < 3 2   o u   x > 2

Resposta

f ( x ) < 0                     s e   x < - 1   o u   3 2 < x < 2 = 0   s e   x = - 1   o u   x = 3 2   o u   x = 2 > 0                   s e   - 1 < x < 3 2   o u   x > 2

Exercícios de Livros Relacionados

Demonstrar:Se 0ab , então sqrt(a b)(a + b)/(2) .
Use um gráfico para encontrar um número δ tal que se 5x5 + δ ent��o x ² x - 5100 ²