Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inequações produto-quociente

Ver Teoria
Exercício 17123456789101112131415161819202122232425262728293031323334353637383940414243444546

Enunciado

UFF, Cálculo IA-Lista 1, GMA, 2008-1, 27

Estude a variação do sinal da função.

f x = x 2 x - 1 x + 1

Passo 1

Pra começar, vamos analisar o sinal de x .

x = 0 → x = 0

x < 0 → x < 0

x > 0 → x > 0

Passo 2

Agora o sinal de 2 x - 1

2 x - 1 = 0 → x = 1 2

2 x - 1 < 0 → x < 1 2

2 x - 1 > 0 → x > 1 2

Passo 3

x + 1 = 0 → x = - 1

x + 1 < 0 → x < - 1

x + 1 > 0 → x > - 1

Vale lembrar que x + 1 é o denominador da função, logo quando ele se torna nulo a função não está definida.

Passo 4

Agora vamos juntar tudo no quadro de sinais.

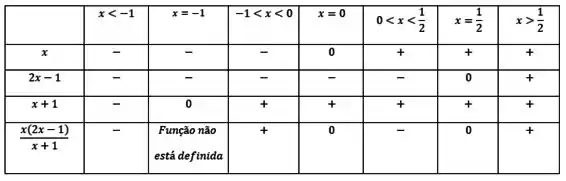
Então o sinal de f varia assim:

f ( x ) < 0                     s e   x < - 1   o u   0 < x < 1 2 = 0                                           s e   x = 0   o u   x = 1 2   > 0                   s e   - 1 < x < 0   o u   x > 1 2

Resposta

f ( x ) < 0                     s e   x < - 1   o u   0 < x < 1 2 = 0                                           s e   x = 0   o u   x = 1 2   > 0                   s e   - 1 < x < 0   o u   x > 1 2

Exercícios de Livros Relacionados

Demonstrar:Se 0ab , então sqrt(a b)(a + b)/(2) .
Use um gráfico para encontrar um número δ tal que se 5x5 + δ ent��o x ² x - 5100 ²