Resolva:
Passo 1
Vamos lá. Lembre-se primeiro que não podemos usar produto cruzado aqui, portanto, vamos jogar tudo no mesmo lado:
Juntando tudo no mesmo denominador:
Passo 2
Agora, pegamos as expressões relevantes, marcamos seus zeros e fazemos uma tabela de sinais:
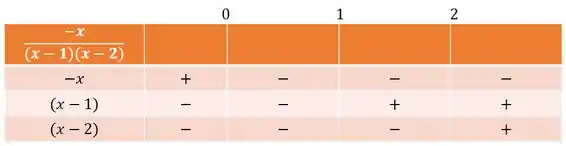
Agora, fazendo estudo do sinais, vemos o sinal da expressão:
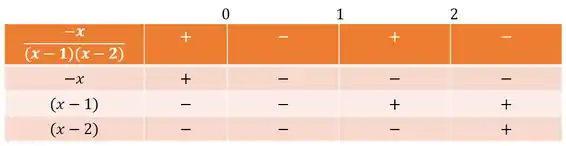
Como queremos:
Pegamos os valores negativos e, portanto, a solução é:
Resposta
Exercícios de Livros Relacionados
Demonstrar:Se 0ab , então sqrt(a b)(a + b)/(2) .
Use um gráfico para encontrar um número δ tal que se 5x5 + δ ent��o x ² x - 5100 ²