Resolva a inequação a seguir e apresente o quadro de sinais e os possíveis valores de x.
Passo 1
Vamos lá!! Temos nessa questão uma inequação envolvendo um produto:
Onde e
Vamos encontrar as raízes deles e montar a tabelinha marota!
Passo 2
Analisando , temos
Visualmente teremos
Analisando , temos
O esboço seria
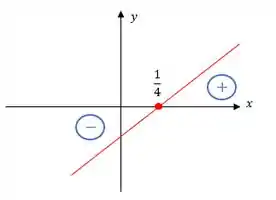
Beleza?!
Passo 3
A partir desses valores, vamos montar a tabelinha para estudar os sinais:
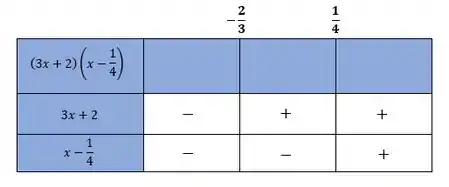
Agora fazendo o estudo dos sinais, teremos
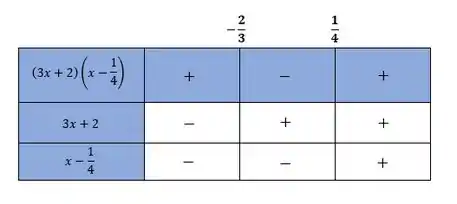
Como queremos
Vamos selecionar os intervalos aonde o sinal é positivo! Assim, nosso conjunto solução é
Resposta
Exercícios de Livros Relacionados
Demonstrar:Se 0ab , então sqrt(a b)(a + b)/(2) .
Use um gráfico para encontrar um número δ tal que se 5x5 + δ ent��o x ² x - 5100 ²