Qual a solução da inequação abaixo?
Passo 1
Vamo que vamo!
Para início de conversa, vamos estudar o sinal da função:
Depois, iremos ver para que intervalo do domínio,
Só que, antes, teremos que definir o domínio de .
Passo 2
A única restrição ao domínio de é o denominador, já que a função não apresenta raízes, nem logaritmos, nem nada. Vamos olhar para o denominador:
Passo 3
Hora de analisar o sinal da função. Repare que a função já está toda fatorada em monômios do primeiro grau: .
Vamos analisar o sinal desses monômios separadamente e depois usar a tabelinha. Para analisar, basta achar as raízes e ver se a função é crescente ou decrescente.
Analisando :
A função é decrescente, então, é positiva antes de e negativa depois de .
Analisando :
A função é crescente, então, é negativa antes de e positiva depois de .
Analisando :
A função é crescente, então, é negativa antes de e positiva depois de .
Passo 4
Hora de usar a tabelinha!
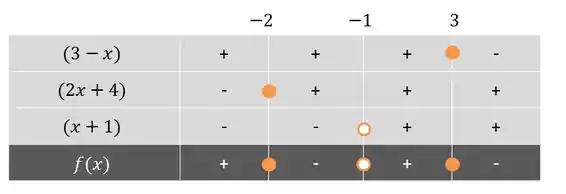
Repare que representei com bolinhas fechadas as raízes (zeros da função) que pertencem ao domínio e com bolinhas abertas, as raízes que não pertencem ao domínio.
Resposta
Como queremos , o intervalo solução é: