UFPA, Sem Campus, Cálculo I, Listas de Cálculo 1 - Profº Luiz Gutemberg - Lista 01, Questão 1e
Resolva as inequações:
e)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente resolver a inequação que ele nos deu. Repare que temos um produto de equações formando essa desigualdade.
E quando temos um produto ou um quociente na inequação precisamos fazer a análise de sinal de cada termo, de modo que a condição da desigualdade seja satisfeita.
Então, vamos encontrar as raízes de cada termo, analisar seus sinais e depois montar o quadro de sinais para encontrar nossa solução.
Vamos lá!
Passo 2
Nossa inequação é dada por:
O primeiro termo é e o segunto termo é . Para o primeiro, sua raiz será apenas:
E no segunto termo, teremos a raiz:
Como o é positivo em ambas as funções, ela será crescente e terá valores negativos antes da raiz e terá valores positivos depois. Então, juntando isso no quadro de sinais, temos:
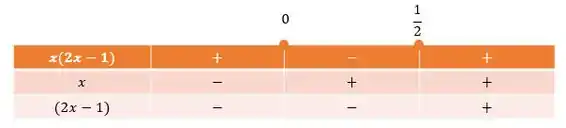
Recapitulando: que nós fizemos foi colocar a função junto com as expressões que a compõe na primeira coluna. Verificamos que por ser positivo em ambas as expressões, o sinal será negativo antes das raízes e positivo depois. E por fim, fizemos o jogo de sinais na primeira linha (sinais diferentes , sinais iguais ).
Como nossa condição é de que a função seja maior ou igual a zero, ou seja, positiva ), nossa solução será a parte da tabela onde temos o sinal positivo na primeira linha. Assim, temos:
Também podemos escrever na forma de intervalo:
Prontinho, galera! Até a próxima! 😉