7) Calcule o fluxo do campo , através da superfície aberta , com tendo componente positiva.
Passo 1
Se o problema nos pediu fluxo de sobre uma superfície , com toda certeza o que ele está buscando é que façamos uma integral de superfície:
Para resolver essa integral, poderíamos seguir basicamente 2 caminhos:
1º - Fazer de uma forma direta (parametrizando e tudo mais)
2º - Aplicar o Teorema de Gauss.
Veja você que o campo é um pouco complicado para se fazer uma integral de superfície direto com ele. Além disso, se você quer mais certeza ainda que de fato vamos resolver o problema pelo Teorema de Gauss, calcule o divergente...
Como
Calculando as derivadas parciais:
Logo...
Pow, com um divergente simples e convidativo (se parece com a equação da esfera) sim, o problema está pedindo que façamos por Gauss!
Passo 2
O teorema basicamente é a igualdade maravilhosa:
Mas não podemos aplicar essa integral assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:
1º - Uma superfície fechada delimitando o sólido :
2º - Sem singularidades na função Vetorial:
3º - Superfície orientada positivamente:
Vem comigo averiguar essas condições ;D
Passo 3
1º - Uma superfície fechada delimitando o sólido :
Veja que ela nos representa uma esfera que termina em da boca pra baixo. Infelizmente ela é uma superfície aberta, logo, para aplicar o Teorema teremos que fecha-la. Podemos fazer isso com o plano ...
Veja então que o sólido onde devemos integrar agora é fechado pelas superfícies e por esse plano que vamos chamar de , logo...
Como queremos o fluxo só em , isolemos...
Passo 4
2º - Sem singularidades na função Vetorial:
Esse campo Vetorial funciona em todas as situações, afinal ele não tem nenhuma divisão por ou algo do tipo.
3º - Superfície orientada positivamente:
Bem, isso significa que precisamos de uma superfície com vetores normais saindo do sólido fechado por ela, o que já acontece lá do enunciado, afinal o vetor tem a componente positiva...
Passo 5
Bem, com as três condições sendo satisfeitas, podemos aplicar a igualdade do Teorema sem nenhuma restrição...
Então se queremos a integral de superfície , calculemos a integral tripla e essa integral de superfície em cima de . Eu sei, parece insano isso neh? Trocando uma integral para resolver duas... Mas cara, acredite em mim, essa é a maneira ais rápida que temos !
Passo 6
Então vamos lá, e começando com a integral tripla...
Descrevendo :
Como estamos falando de um pedaço de uma esfera, podemos utilizar as mudanças para coordenadas esféricas:
Onde o Jacobiano dessa mudança é:
E uma equação que nos ajuda muito é a equação da esfera:
Passo 7
Não devemos sair de uma mudança de coordenadas sem antes dizer onde os parâmetros variam:
Para encontrar a variação de e , devemos olhar pra projeção do sólido no plano ...
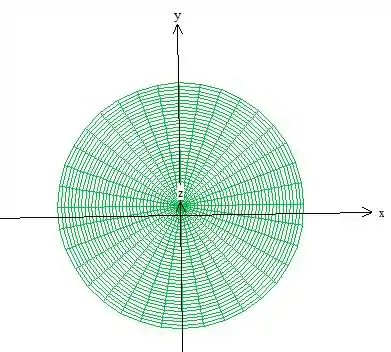
Veja que essa projeção se parece muito pelo método gráfico com um círculo. Não podemos ficar no “se parece” neh? Devemos ter certeza, por isso vamos encontrar a equação dessa projeção.
Observe que ela é o encontro da equação do plano com a equação do cone:
Veja que a intersecção de fato é uma circunferência de raio , onde podemos concluir que o Raio ...
E o ângulo ...
Já variação do , bem ele é o cara que varia de cima pra baixo no sólido:
Passo 8
Então montando a integral tripla não se esquecendo do Jacobiano...
Resolvendo a integral de dentro achamos:
Eu sei que é tentador terminar a questão aqui, mas não se esqueça de que ainda não chegamos ao valor do fluxo em , então...
Passo 9
Vamos calcular agora a integral de superfície em ...
foi a superfície que adicionamos para tampar o buraco, ou seja é o plano ...
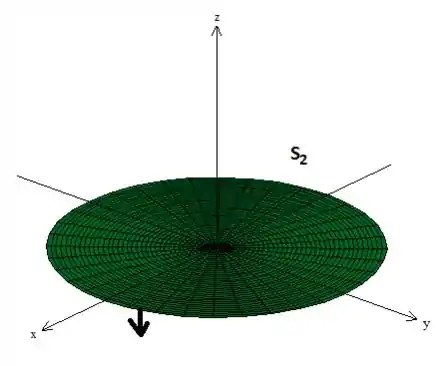
Essa superfície tem o vetorzinho normal apontado para baixo e ele é unitário, então...
Logo...
Como no plano o é , então...
Substituindo na integral de superfície...
Bem, ficou vezes a área de . Ora bolas, não é uma circunferência de raio ?...
Passo 10
Regressando a integral do problema...