Calcule
Onde e é a superfície , orientada pela normal que satisfaz .
Passo 1
Temos uma função muito louca com logaritmo arco tangente, se tentarmos fazer essa integral de superfície da forma normal vai dar uma treta braba.
Então vamos tentar usar o teorema de Gauss, para isso temos que ver se a função é definida dentro da superfície e precisamos de uma superfície fechada.
Se olharmos vemos que teríamos problemas se o cara dentro do logaritmo fosse negativo, mas dentro do ln temos que sempre será positivo, então não temos problemas com a função .
Vamos ver agora como é a superfície , repara que temos um paraboloide circular. O gráfico vai ficar
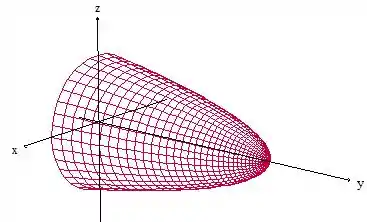
Repara que esse paraboloide não é fechado, então precisamos fechar essa superfície para aplicar Gauss. Basta tampar na base desse paraboloide, ou seja, seria a parte onde
Isso seria
Com
Então vamos fazer
Onde é o paraboloide e é
Aplicando Gauss teríamos uma parada assim
Onde é o sólido com fronteira sendo que definimos ali.
Fica atento na orientação que ele quer, , isso quer dizer que a componente em é positiva, se olharmos o gráfico ali em cima do nosso paraboloide, podemos perceber que isso quer dizer fora desse paraboloide. Assim o vetor é fora do sólido .
Passo 2
Vamos agora calcular o divergente dessa função
Vamos agora escrever aquela equação do teorema de Gauss deixando direitinho tudo que precisamos fazer
Lembrando que
Então
Vamos precisar fazer a integral de Superfície de e a integral tripla em .
Vamos fazer cada parte em separado.
Passo 3
Vamos começar com a integral de Superfície em , primeiro temos que achar o vetor normal.
Repara que é a parte do plano limitada por
Então vamos fazer
E o vetor normal vai ser
E esse vetor é unitário, não precisamos nos preocupar em normalizar ele. Além disso, a orientação dele está errada né? Queremos para fora do sólido, então essa parte de baixo precisa que seja negativa isso porque ela é a parte de baixo, então
A nossa integral vai ficar
Repara que temos , então
Passo 4
Vamos agora resolver essa integral dupla. Para isso vamos usar coordenadas polares, só que aqui temos
Então vamos fazer
Passo 5
A equação de é
Isso nos diz que isso é uma circunferência de raio então vamos ter
Passo 6
A nossa integral dupla vai ficar
Vamos fazer
A nossa integral vai ficar
Passo 7
Vamos agora para a integral tripla
Para essa região vamos usar coordenadas cilíndricas, isso porque vai de ao paraboloide e vamos ter e se mantendo dentro de
Então vamos fazer
Repara que colocamos em vez de isso porque o eixo dessa nossa coordenada cilíndrica, nesse caso, é o , fora isso tudo fica igual.
Passo 8
Vamos ter e limitados dentro da circunferência então
Vamos agora ver como fica , ele vai de ao paraboloide, então ele vai ser
Trocando as coordenadas cilíndricas vamos ter
Passo 9
A integral tripla vai ficar
Passo 10
Lembrando que
Vamos trocar os valores que achamos