Questão 2: Calcule o fluxo
Do campo vetorial
Através da superfície definida como sendo a porção da esfera satisfazendo a condição orientada com o vetor norma apontando para fora da esfera.
Passo 1
Bem, o que vamos calcular aqui é uma integral de superfície vetorial de um campo em cima de uma superfície :
Poderíamos tentar calcular na marra de forma direta (parametrizando e tudo mais)? Poderíamos! Mas aqui em integrais de superfície a gente precisa ser sagaz para evitar muuuuuitas contas, não é mesmo? Então, devido ao fato de o campo ser feio, vamos tentar resolver por outro método:
O teorema de GAUSS
O teorema que nos dá uma igualdade maravilhosa entre uma integral de superfície e uma integral tripla:
Passo 2
Eu sei! Quem disse que trocar a integral de superfície por uma integral tripla vai facilitar a nossa vida? Nem sempre facilita, por isso se você tiver dúvida se aplica ou não Gauss, sugiro que calcule o divergente primeiro:
Onde , e são componentes de ...
Calculando as derivadas então...
POW! Um divergente bonito como esse, sem qualquer variável no meio, só pode nos estar pedindo para resolver com Gauss ! Bora?
Passo 3
Mas calma lá, jovem! Antes de aplicarmos o teorema em si, devemos verificar se estamos nas condições que o Teorema nos exige:
- Ter uma superfície fechada delimitando um sólido (cuja fronteira a gente chama de ).
- Ter uma orientação positiva.
- E por último, um campo sem singularidades.
Nos próximos três passos, vamos avaliar cada um deles, ok?
Passo 4
A primeira condição exige uma superfície fechada. Vamos ver se isso é verdade no enunciado:
“... superfície definida como sendo a porção da esfera satisfazendo a condição ...”
Bem, então a nossa superfície está em cima dessa esfera de raio aqui:
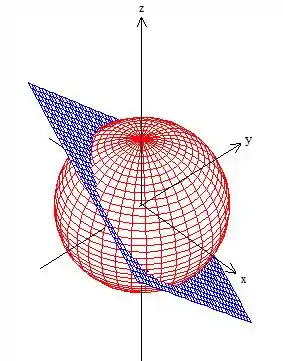
Mas atenção! A superfície não é essa esfera toda aí não, tá? Afinal a condição , pega apenas os pontos da esfera que estão em cima desse plano aí:
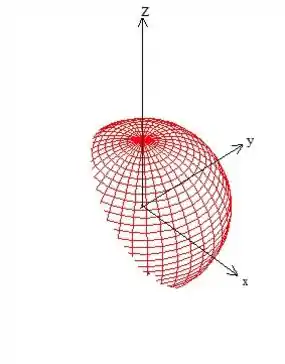
E no final das contas sobra a nossa superfície que queremos o valor do fluxo:
É importante ressaltar também que para aplicar o teorema precisamos de um sólido , e o sólido é justamente o interior dessa calota polar aí. Essa região tem como bordas () a superfície vermelha e o disco do plano (que também fecha a calota em baixo, saca?):
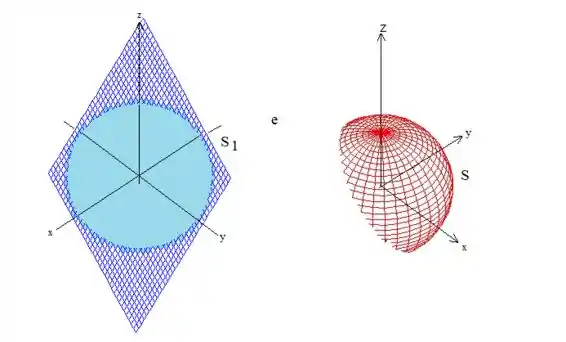
Se chamarmos esse disco vermelho de (Só um nome rsrs), isso que acabamos de falar em notação matemática é:
Passo 5
Sobre a orientação, a segunda condição do Teorema, bem... Isso se refere ao vetor normal. Pera estar orientado positivo, ele deve estar saindo do sólido, e vejamos o que o problema nos disse sobre ele:
“... orientada com o vetor norma apontando para fora da esfera.”
Pow! Pelo próprio enunciado, o vetor está apontando para fora da esfera, o que significa que ele está apontando para fora da nossa calota também:
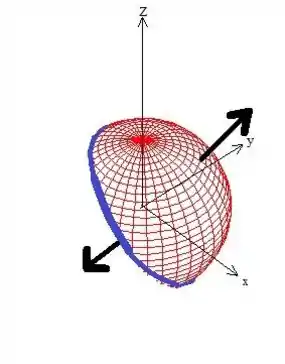
E essa já é a orientação positiva , sacou?
Passo 6
Só falta verificarmos se o campo não tem nenhuma singularidade onde estamos trabalhando:
Veja que esse campo funciona em qualquer ponto do espaço, logo... Ele não tem singularidades alguma ;)
Passo 7
Com as três condições vistas e sendo satisfeitas, podemos finalmente aplicar o teorema sem medo de ser feliz:
Mas veja que a borda de é a gora a união de duas superfícies:
Então...
A nossa intenção desde o início foi de calcular o fluxo em cima de (a esfera), logo, vamos isolar e calcular as duas integrais que apareceram. Eu sei que pode parecer doidera o que estamos fazendo, mas vai por mim, é quase sempre o jeito mais easy mesmo .
Passo 8
Vamos começar com a integral tripla:
Bem, a integral tripla de é o volume, e cara para a nossa sorte, trata-se de uma calota, então sabemos calcular o volume sem precisar jogar na integral, neh? Eu quero que olhe para a calota e se convença de que se trata exatamente da metade da esfera:
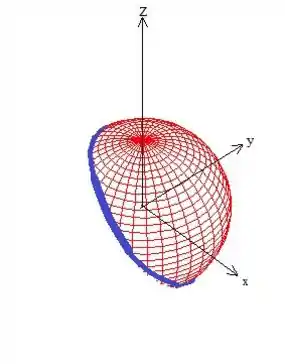
Aí você poderia se perguntar: “Mas o que garante isso?”. É uma boa pergunta e a resposta é que: a esfera está centralizada na origem e o plano que corta a esfera passa exatamente por esse ponto:
O que prova que o plano de fato passa pela origem. E agora é que vem a graça: toda plano que passa pelo seu centro, corta a esfera em duas partes iguais !
Então...
Passo 9
Estamos prontos para enfrentar a outra integral de superfície agora:
Veja que essa integral de superfície aqui é uma integral em cima do disco que o plano fez com a esfera (por isso as contas vão ser fáceis, quer ver?). Vamos resolvê-la de forma diretona:
- Primeiro a parametrização:
- Mas agora é hora de encontrar o termo ...
- Substituindo na integral de superfície...
Logo, a parametrização, pode ser dada de forma explicita onde os parâmetros são os próprios e :
Esses parâmetros estão presos dentro da esfera! Caso precise, a gente ver onde eles estão variando direitinho ;)
e
Esse vetor normal tem um bizu para encontra-lo quando a parametrização é em função de e assim:
Outra observação é que temos que ter cuidado, pois esse vetor normal aí ta apontado pra cima e queremos o que aponta pra baixo, como vimos, então...
Como pela própria superfície ...
Epa! Integral de é a área da superfície. Como a superfície (O disco) tem raio ...
Passo 10
Assim, voltando para a integral que a gente realmente quer (depois de ter calculado duas que a gente não quer):