Seja .
- Calcule .
- Seja , onde é a superfície do paraboloide limitado pelo plano , com vetores normais apontando para fora. Mostre que , usando:
b1) o Teorema de Gauss.
Passo 1
Letra a)
Vamos começar calculando esse rotacional ai
Passo 2
Letra b)
Agora, precisamos mostrar que:
Onde é o paraboloide cortado pelo plano .
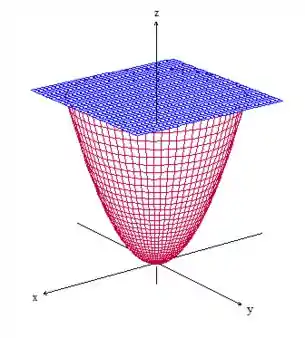
Passo 3
Letra b1)
Aplicando o Teorema de Gauss, podemos trocar uma integral em uma superfície fechada por uma integral tripla no volume limitado por essa superfície.
Porém, não é fechada. A superfície do problema é o paraboloide cortado, que é aberto!
Logo, precisamos fechar essa superfície antes de aplicar o teorema.Vamos fechar com o próprio disco plano que corta o paraboloide, para simplificar as coisas.
Então, sendo as superfícies orientadas positivamente (normais apontam para fora), temos:
Sendo :
Onde é o paraboloide cortado, é o disco plano que “fecha” a superfície e é o volume limitado por e . Foi?
Passo 4
Agora vamos calcular esse divergente aí:
O que nos dá:
Precisamos, então, da integral em .
Passo 5
Para encontrar a equação desse disco , vamos fazer na equação do paraboloide:
Portanto, se trata de um círculo de raio em . Vamos, então, usar coordenadas polares, ok?
Onde e .
Agora, vamos achar a normal a essa superfície:
Como a normal aponta para fora de e, para o disco, isso significa , sabemos que encontramos o vetor certo.
Passo 6
Agora vamos trazer tudo o que achamos para a fórmula:
Onde:
Nem escrevemos as duas primeiras componentes do rotacional porque elas vão cancelar quando for feito o produto escalar com a normal!
Resolvendo isso aí:
Passo 7
Calma que ainda não acabou! Lembra que
Agora sim!
Resposta
Ei, a resposta está no passo a passo :)