Seja a parte da superfície esférica , com , orientada pela normal unitária (exterior à esfera). O valor da integral de superfície
é igual a:
a)
b)
c)
d)
e)
Passo 1
Cara, a gente tem um campo vetorial bem feio, uma superfície com vetor normal externo e precisamos calcular uma integral de superfície. Essas são dicas para gente calcular essa integral usando o teorema de Gauss!
Vamos começar calculando o divergente de para saber se nossa ideia é boa mesmo. Ele tem essa fórmulinha:
Como o nosso campo é:
Então a gente calcula:
Nossa o divergente está bem simples. Outra dica de que vamos de Gauss. Vem comigo!
Passo 2
Cara, Gauss tem umas condições para aplicar. Duas delas já atendemos:
- nosso campo está bem definido em todo (já que não temos nenhuma restrição no domínio, tipo um denominador que pode zerar).
- o vetor normal à semiesfera aponta para fora dela, e a esfera é uma superfície lisa.
Maaas, a gente não atende um critério muito importante: temos a equação de uma esfera, mas , ou seja, é só a metade de cima da esfera. Isso significa que a nossa superfície não está fechada.
O que a gente faz? Chora? Não! A gente vai fechar essa semiesfera. Com um plano em formato circular, porque planos são simples. Aí a nossa superfície geral vai ser a metade da esfera e esse plano, beleza?
Podemos parametrizar esse plano como:
A componente dele em é nula porque ele está em no espaço. Agora repara aqui nesse gráfico lindão:
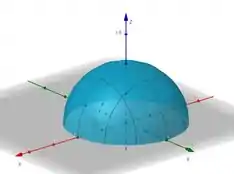
Repara que o nosso plano, para fechar a essa superfície, precisa ter o formato da interseção da semiesfera com o plano , certo? A equação dela é:
Ou seja, uma circunferência. Nosso plano vai estar dentro dessa circunferência. Então a gente pode dizer que o domínio dele é:
Passo 3
Agora vamos montar nossa equação pelo teorema de Gauss. Ele diz que:
Esse é uma superfície fechada. No nosso caso, a superfície fechada é a soma de duas superfícies. A semiesfera e o nosso plano . Então a gente pode reescrever essa parte assim:
Lembra que nosso divergente deu 1:
A integral tripla de 1 é o volume do domínio . No nosso caso, esse domínio é a metade de uma esfera de raio . A gente consegue calcular isso tranquilinho pela fórmula de volume da esfera:
Então isolamos quem a gente quer achar:
Só falta calcular essa integral de superfície sobre o plano. Então vamos focar nela!
Passo 4
O campo é aquele estranho né:
A nossa parametrização do plano é:
Esse vai ser o domínio da nossa integral.
A gente precisa começar achando o vetor normal a esse plano. Mas repara que esse plano está dentro de . O vetor normal a todo o é o vetor , que é o sentido do eixo , certo?
Então esse vai ser o nosso vetor? Cara, ele com certeza é normal a nossa superfície, mas ele está apontando para fora da nossa semiesfera? Olha ele:
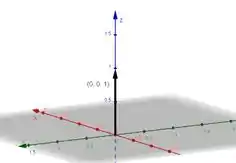
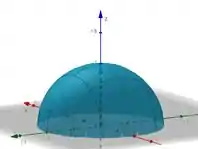
Ele está apontando para dentro da semiesfera. Para apontar para fora, ele precisa estar apontando no sentido oposto. Então só vamos multiplicar ele por :
Aí o nosso integrando fica:
A gente precisa substituir as componentes do plano aí.
Passo 5
Nossa integral ficou assim:
A integral dupla sobre esse círculo de raio 1 vai ser igual a área do círculo! Isso porque o argumento dela é . Como a área do círculo é e :
Voltando para Gauss:
Resposta
Letra b