Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Superfície Aberta

Ver Teoria
Exercício 2412345678910111213141516171819202122232526272829303132333435363738394041424344454647

Enunciado

Considere o campo vetorial

F → x ,   y ,   z = 2 x z + z cos ⁡ y ,   e x - 2 z ,   8 y 2 .

  1. Calcule o fluxo de F → através do disco D dado pela interseção da esfera x 2 + y 2 + z 2 ≤ 2 com o plano z = - 1 , orientado para cima.
  2. Determine o divergente de F → .
  3. Calcule o fluxo de F → através do pedaço S da superfície esférica x 2 + y 2 + z 2 = 2 que se situa acima do plano z = - 1 , orientada pela normal exterior.

Passo 1

Letra a) Vamos começar esse problema, entendendo um pouco mais sobre o disco D .

Sabemos que ele está sendo dado pela interseção da esfera x 2 + y 2 + z 2 ≤ 2 , que tem raio 2 , com o plano paralelo ao plano X Y passando por z = 1 .

Desenhando essas duas coisas juntas no espaço, teremos

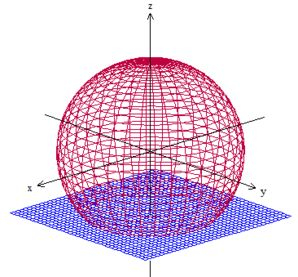
No caso, como o problema nos pediu o disco, a superfície D será essa em cima do plano dentro da esfera

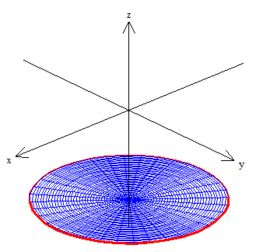
Calcular o fluxo do campo F → por esse disco é apara a gente aqui calcular a integral de superfície

∬ D   F → ∙ n →   d S

Então vem comigo!:)

Passo 2

Antes de tudo, devemos procurar uma parametrização para a nossa superfície D .

Como essa superfície é esse disco por cima do plano z = - 1 , podemos então pensar numa parametrização explícita:

x = x

y = y

z = - 1

Ou seja, uma boa parametrização para o plano é

φ x ,   y ,   z = x ,   y ,   - 1

Percebeu?

Como toda e qualquer parametrização, onde esses parâmetros x e y estão variando?

Bem, pra isso utilizamos a restrição: não queremos o pedaço do plano restrito dentro da esfera x 2 + y 2 + z 2 ≤ 2 ? Sim! E como no plano temos z = - 1 , substituindo...

x 2 + y 2 + - 1 2 ≤ 2       ⇒         x 2 + y 2 + 1 ≤ 2         ⇒

x 2 + y 2 ≤ 1

Ou seja, queremos x e y dentro da equação x 2 + y 2 = 1 que representa um círculo de raio 1 :

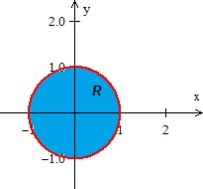
Chamamos essa região de R .

Passo 3

Bem, antes de partirmos para as contas, precisamos encontrar aquele vetor normal N → da superfície.

Pow! Aqui, basta usar o bizu de parametrização explícita do tipo z = z x ,   y = - 1 , ou seja,

N → x ,   y = - ∂ z ∂ x ,   - ∂ z ∂ y ,   1       ⇒

N → x ,   y = 0 ,   0 ,   1

Lembrando que n →   d S = N →   d x d y , teremos n → d S = 0 ,   0 ,   1 d x d y , voltando para a integral e substituindo tudo, teremos

∬ D   F → ∙ n →   d S = ∬ R   2 x z + z cos ⁡ y ,   e x - 2 z ,   8 y 2 ∙ 0 ,   0 ,   1 d x d y =

Fazendo esse produto interno

∬ R   8 y 2 d x d y

Agora é só calcular essa integral dupla aí e partir para o abraço!

Passo 4

Como estamos dentro de R , uma região circular, vamos fazer uma mudança para coordenadas polares

x = r cos ⁡ θ

y = r cos ⁡ θ

J = r

Onde olhando para a região, notamos que o raio...

0 ≤ r ≤ 1

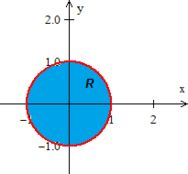
E o ângulo theta dá uma volta completa, ou seja,

0 ≤ θ ≤ 2 π

Logo,

∬ R   8 y 2 d x d y = 8 ∫ 0 2 π ∫ 0 1 r sin ⁡ θ 2 ∙ J d r d θ =

8 ∫ 0 2 π ∫ 0 1 r 3 sin 2 ⁡ θ d r d θ

Integrando primeiro em r

8 ∫ 0 2 π sin 2 ⁡ θ r 4 4 0 1 d θ =

8 4 ∫ 0 2 π sin 2 ⁡ θ d θ

Lembrando que sin 2 ⁡ θ = 1 - sin ⁡ 2 θ 2

2 ∫ 0 2 π 1 - sin ⁡ 2 θ 2 d θ = ∫ 0 2 π 1 - sin ⁡ 2 θ d θ

Integrando aí lembrando que cos ⁡ 2 θ ' 2 = - sin ⁡ 2 θ

∫ 0 2 π d θ + ∫ 0 2 π cos ⁡ 2 θ ' 2 d θ =

Integrando isso aí, lembrando que ∫ 0 2 π cos ⁡ 2 θ ' 2 d θ = cos ⁡ 2 θ 2 pelo t e o r e m a   d o   c á l c u l o

θ 0 2 π + 1 2 cos ⁡ 2 θ 0 2 π =

Substituindo esses caras, ganharemos

∬ D   F → ∙ n →   d S = 2 π

Passo 5

Letra b) Para o cálculo do divergente, não tem mistério, basta aplicar a fórmula

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z

Como F → = F 1 ,   F 2 ,   F 3 = 2 x z + z cos ⁡ y ,   e x - 2 z ,   8 y 2 , calculando essas derivadas parciais...

∂ F 1 ∂ x = ∂ 2 x z + z cos ⁡ y ∂ x = 2 z

∂ F 2 ∂ y = ∂ e x - 2 z ∂ y = 0

∂ F 3 ∂ z = ∂ 8 y 2 ∂ z = 0

E jogando no divergente

d i v   F → = 2 z + 0 + 0 = 2 z

Passo 6

Letra c) Então, agora devemos encontrar o fluxo através do pedaço da esfera acima do plano z = - 1

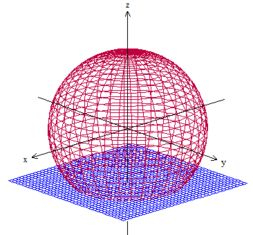
Como já determinamos o divergente, podemos tentar resolver esse problema por teorema de Gauss. Bora então?

Passo 7

Gauss nos fala o seguinte:

∬ ∂ E   F → ∙ n → d S = ∭ E   d i v   F → d V

Esse ∂ E é a borda do sólido E que esta acima do plano e abaixo da esfera, ou seja, é a união do disco D com S (o pedaço da esfera que queremos), logo

∬ ∂ E   F → ∙ n → d S = ∬ D   F → ∙ n → d S + ∬ S   F → ∙ n → d S

Então, substituindo em Gauss

∬ D   F → ∙ n → d S + ∬ S   F → ∙ n → d S = ∭ E   d i v   F → d V

Mas note que essa integral ∬ D   F → ∙ n → d S , não é a mesma que calculamos, é a inversa negativa dela! What????

Calma!

Olha só, calculamos essa integral com o vetor apontando pra cima.

Como agora queremos com o vetor pra baixo (pois todos vetores devem estar saindo do sólido), apenas inverteremos o sinal, percebeu?!:)

Logo

- ∬ D   F → ∙ n → d S + ∬ S   F → ∙ n → d S = ∭ E   d i v   F → d V         ⇒

∬ S   F → ∙ n → d S = ∭ E   d i v   F → d V + ∬ D   F → ∙ n → d S   ⇒  

∬ S   F → ∙ n → d S = ∭ E   d i v   F → d V + 2 π

Bem, de integral de superfície, mão tem mais nada. Basta resolver essa integral tripla aí e o nosso problema acaba!

Passo 8

Para resolver essa integral tripla no sólido E : ∭ E   2 z d V , vamos precisar prestar muita atenção, pois essa integral não é simples de se resolver, beleza?

Para facilitar, a gente vai dividir o sólido E em duas partes um pouco mais fáceis:

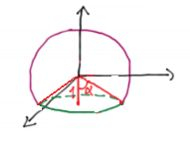
Ou seja, dividimos em um pedaço de esfera em rosa, e um cone em vermelho.

Qual que é o legal de fazer isso, é que podemos dividir aquela integral tripla em duas partes também:

  • Uma integral que a gente poderá usar coordenadas esféricas (na parte da esfera rosa)

    • x = R sin ⁡ φ cos ⁡ θ

    y = R sin ⁡ φ sin ⁡ θ

    z = R cos ⁡ φ

    J = R 2 sin 2 ⁡ φ

    onde o raio R varia de 0 até 2 , o ângulo θ varia de 0 até 2 π e o ângulo φ varia de 0 até o ângulo máximo que a gente vai ver qual é.

  • A outra integral, na parte do cone, poderemos resolver por uma substituição cilíndrica:

x = r sin ⁡ ϕ

y = r cos ⁡ ϕ

J = r

Então vamos nessa?

Passo 9

Vamos começar com o pedacinho de esfera rosa.

Sabemos que vamos usar coordenadas esféricas, mas qual é os limites dessas variáveis aí mesmo?

Bem, o raio R , ele simplesmente sai da origem e vai até o raio máximo da esfera:

0 ≤ R ≤ 2

θ é aquele ângulo que varia no plano x y , e portanto ele deve dar uma volta completa:

0 ≤ θ ≤ 2 π

Quanto ao φ , ele varia de cima pra baixo no eixo z , então ele começa no ângulo 0 e vem até aquela retinha vermelha.

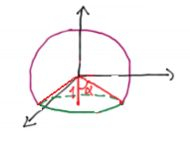
Se lembrarmos de que essa circunferência verdinha tem raio igual a 1,

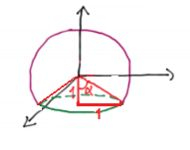
Logo esse ângulo α , só pode ser de 45 º , ou π 4 · Então o ângulo φ

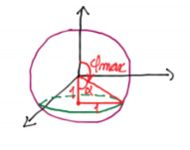
Será o seu complementar, ou seja

φ = π - π 4 = 3 π 4

Logo

0 ≤ φ ≤ 3 π 4

Passo 10

Resolvendo a integral tripla em cima dessa esfera, lembrando-se de multiplicar a função pelo jacobiano das eféricas, teremos

∫ 0 2 π ∫ 0 3 π 4 ∫ 0 2 2 z ∙ J   d R d φ d θ

Substituindo z pelos da parametrização e substituindo o jacobiano...

∫ 0 2 π ∫ 0 3 π 4 ∫ 0 2 2 R cos ⁡ φ ∙ R 2 sin ⁡ φ d R d φ d θ =

∫ 0 2 π ∫ 0 3 π 4 ∫ 0 2 2 R 3 cos ⁡ φ ∙ sin ⁡ φ d R d φ d θ

Integrando primeiro em R

∫ 0 2 π ∫ 0 3 π 4 2 cos ⁡ φ ∙ sin ⁡ φ R 4 4 0 2 d φ d θ =

Substituindo os limites

∫ 0 2 π ∫ 0 3 π 4 2 cos ⁡ φ ∙ sin ⁡ φ 4 4 d φ d θ =

∫ 0 2 π ∫ 0 3 π 4 2 cos ⁡ φ ∙ sin ⁡ φ d φ d θ

Lembrando se de que 2 cos ⁡ φ ∙ sin ⁡ φ = sin ⁡ ( 2 φ ) ,

∫ 0 2 π ∫ 0 3 π 4 sin ⁡ ( 2 φ ) d φ d θ =

∫ 0 2 π - cos ⁡ 2 φ 2 0 3 π 4 d θ =

∫ 0 2 π - cos ⁡ 2 ∙ 3 π 4 2 - - cos ⁡ 2 ∙ 0 2 d θ

Simplificando

∫ 0 2 π - cos ⁡ 3 π 2 2 - - cos ⁡ 0 2 d θ

Como - cos ⁡ 3 π 2 = 0

∫ 0 2 π - cos ⁡ 3 π 2 2 - - cos ⁡ 0 2 d θ = ∫ 0 2 π 1 2 d θ =

1 2 2 π - 0 = π

Passo 11

Bem, mas infelizmente não acabou aí! Falta regressarmos na integral, mas agora fazendo para o cone vermelho utilizando a substituição cilíndrica

x = r sin ⁡ ϕ

y = r cos ⁡ ϕ

z = z

Uma equação que pode nos ajudar é a do cilindro

x 2 + y 2 = r 2

O jacobiano nessa substituição vale

J = r

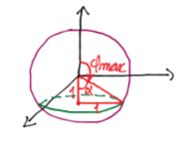
Note que esse cone ele é aquele cone normal que conhecemos de equação z 2 = x 2 + y 2 , porque o ângulo de abertura ali é de 45 º

Passo 12

Vamos encontrar então os limites dessas variáveis aí:

O raio r , varia de 0 ao raio máximo que é delimitado pelo cone vermelho, portanto

0 ≤ r ≤ c o n e   v e r m e l h o

Como o cone é z 2 = x 2 + y 2 = r 2 , extraindo a raiz

0 ≤ r ≤ x 2 + y 2

0 ≤ r ≤ z 2

Bem, não se esqueça de que o cone está na parte onde z é negativo, então

0 ≤ r ≤ z

0 ≤ r ≤ - z

Quanto a z , podemos perceber na figura que ele varia de - 1 até 1

- 1 ≤ z ≤ 0

θ   novamente dá uma volta completa dentro do cilindro

0 ≤ θ ≤ 2 π

Passo 13

Substituindo os limites na integral tripla, mas dessa vez para o cone

∫ 0 2 π ∫ - 1 0 ∫ 0 - z 2 z ∙ J   d r d z d θ =

∫ 0 2 π ∫ - 1 0 ∫ 0 - z z 2 r   d r d z d θ

Integrando em r primeiro

∫ 0 2 π ∫ - 1 0 z   r 2 0 - z d z d θ

Substituindo os limites

∫ 0 2 π ∫ - 1 0 z - z 2 - 0 d z d θ =

∫ 0 2 π ∫ - 1 0 z 3 d z d θ

Integrando em z

∫ 0 2 π z 4 4 - 1 0 d θ =

∫ 0 2 π 0 4 4 - - 1 4 4 d θ =

∫ 0 2 π - 1 4 d θ

- 1 4 2 π - 0 = - 1 2 π

Passo 14

Logo, podemos concluir então que a integral tripla no sólido E inteiro, é a soma do resultado apenas na parte rosa com a parte vermelha do cone

∭ E   2 z d V = π - π 2 =

∭ E   2 z d V = π 2

Regressando para o teorema de Gauss do final do passo 7...

∬ S   F → ∙ n → d S = ∭ E   d i v   F → d V + 2 π

∬ S   F → ∙ n → d S = π 2 + 2 π =

5 π 2

Resposta

Letra a) 2 π

Letra b)   d i v   F → = 2 z

Letra c) 5 π 2