Calcule o fluxo
Do campo vetorial
Através da superfície
Orientada com vetor normal apontando para fora da esfera.
Passo 1
Bem, dá pra ver que esse campo não é nada tranquilo de integrar pela definição, né? Imagina depois de botarmos a parametrização da esfera... Nem pensar!
Vamos fugir disso usando o teorema de Gauss:
Mas a superfície que temos é um parte da esfera só, a parte de cima dessa figura aqui:
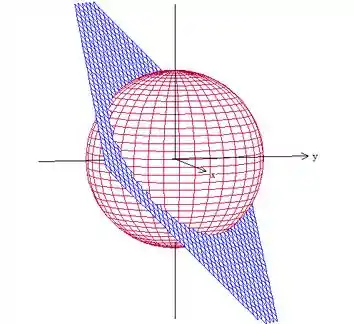
Que como não é uma superfície fechada, não podemos aplicar Gauss diretamente, temos que fechar antes.
Mas podemos simplesmente fechar com o plano da figura:
Então vamos ficar com:
Então vamos ver se conseguimos calcular essas aí agora!
Passo 2
Vamos comçar com a integral tripla. Apesar do campo ser complicado, o divergente é tranquilo de calcular:
O que é muito bom, porque nossa integral fica:
E agora vem um macetinho, mas espero que dê pra entender porque senão fica quase impossível de resolver a questão.
O que a gente tem que perceber é que o plano corta a esfera exatamente na metade, consegue ver? Isso vale pra qualquer plano que passa pela origem que é o que temos nesse caso.
Então vamos ter que:
Passo 3
Bom, vamos para a integral de superfície agora, lembrando que é o plano que fecha a esfera, portanto
Portanto a normal é dada por
Já que queremos que o vetor aponte para fora da esfera!
Aqui vamos ver que, se tentarmos resolver a integral do jeito normal fica bem difícil, vamos ver como fica o produto escalar primeiro:
Que beleza né? Fica mais simples resolver a integral
O que é isso aí? É a área da projeção da superfície no plano , se a gente tentar fazer isso fica bem mais complicado!
A nossa superfície é o círculo de raio dentro da esfera, certo? Essa área sabemos que vale
Então vamos fazer isso aqui, ao invés de usar o vetor normal , vamos usar o vetor unitário . E qual a diferença?
Onde , , logo
Com isso
Agora sim! Essa integral aí é igual a área da nossa superfície que conhecemos! Logo
Passo 4
Ufa! Voltando pro teorema agora pra fechar