Encontre o fluxo do campo através da superfície , orientada positivamente, união das superfícies e , onde é definida por , e tem equação ,
Passo 1
Se liga! O enunciado está pedindo para encontrar o fluxo. Para começarmos a resolver, podemos escrever que o fluxo, que chamaremos de , é dado por
Passo 2
O enunciado pede para achar o fluxo do campo através da união entre as superfícies e , ou seja, .
Outra informação importante é que a superfície é definida por
que representa um paraboloide elíptico com concavidade para baixo com vértice localizado no ponto (). Como ele está definido em , podemos esboçar o desenho dele da seguinte forma.
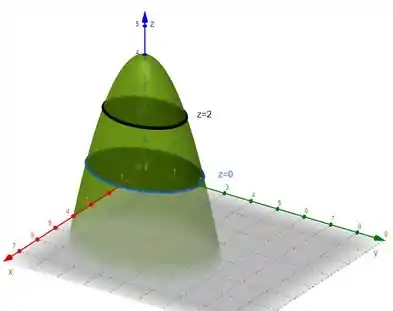
Agora podemos analisar o que acontece quando ,
Chamaremos a superfície deste disco como
Sendo assim, quando temos que
E para
Assim temos duas superfícies que delimitam o sólido em e .
Passo 3
Se considerarmos o plano onde , temos que
Assim, quando ,
e para
Passo 4
A superfície é definida por
no intervalo . Assim podemos esboçar o desenho
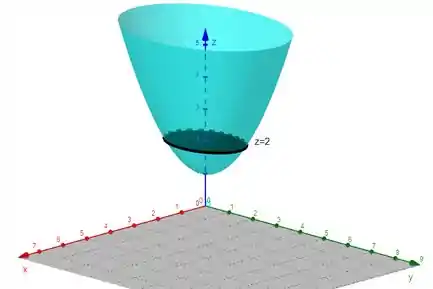
Se liga que quando
Passo 5
Analisando quando , temos
Repare que esta é a mesma equação (1) encontrada para a superfície quando .
Passo 6
Se liga! Quando é feita a união das superfícies, e , no intervalo definido por
a superfície fica por dentro da superfície , sendo assim, quando fazemos
não incluímos a borda superior, quando , da superfície . Repare que não está inclusa em .
Passo 7
Considerando que temos uma superfície fechada, podemos aplicar o Teorema de Gauss.
Onde
Fazendo as derivadas parciais, temos
Passo 8
Podemos separar
Em
Substituindo a (4) em, (2) e usando a equação (3), temos
Passo 9
Agora vamos fazer a parametrização de .
Lembrando que a superfície é definida por
E para ,
No exterior do sólido, temos
Pois aponta para fora.
Como temos todos os elementos necessários, podemos montar a integral
Esta integral é a própria área da superfície , que é uma elipse de raios e . Portanto
Portanto
Passo 10
Agora só precisamos substituir o valor obtido na equação (5). Sendo assim, o fluxo através da superfície é