Calcule o fluxo do campo vetorial
Através da superfície definida por
Com campo vetorial normal tendo componente positiva.
Passo 1
A superfície é quase uma esfera, mas na verdade é só parte dela, mais especificamente, a parte com :
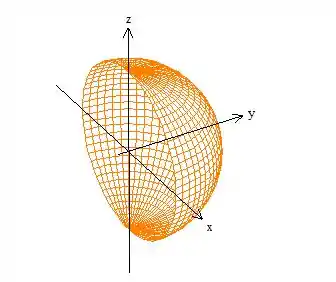
Mas o campo parece meio chato, ainda mais se tentassemos meter uma parametrização esférica aí.. Mas se tentarmos aplicar Gauss, vemos que o divergente:
Então parece uma ótima ideia. Só que Gauss só pode ser usado em superfícies fechadas, né?
Mas isso não é problema, é só nós mesmos fecharmos a superfíe! Nesse caso, a forma mais fácil pra isso parece ser criar uma superfície sendo o plano , com normal com negativo, para respeitarmos a orientação. Aí vamos ter:
Mas já vimos que o divergente é entaõ vai ficar:
Bem, saímos de calcular uma integral sobre um pedaco de esfera, para calcularmos a integra sobre o plano, acho que melhorou já, né? Vamos ver se da pra resolver mesmo!
Passo 2
O que temos que fazer é calcular uma integral de superfície vetorial, entaõ vamos usar a fórmula:
Então primeiro de tudo vamos parametrizar nosso plano, que fica, simplesmente:
Com domínio sendo circulo no plano :
E o normal, por ser no plano , vai ser:
Com orientação negativa, como tinhamos dito lá em cima.
Passo 3
Agora é só jogar na fórmula e vamos ter:
E como tinhamos visto na relação lá em cima:
Tudo isso pra dar zero, sério mesmo?